クラスタリング：k-meansクラスタリング

クラスタリングは、データの特徴量から似ているユーザー・製品・サンプルなどをグループ化する方法です。

様々な手法が存在するクラスタリング手法の中でも、k-meansクラスタリングは扱いが簡単な代表モデルのひとつです。

この記事は「k-meansクラスタリング」についてまとめます。

k-meansクラスタリング

特徴

k-meansクラスタリングは、セントロイドと呼ばれるクラスターの中心点とデータポイントの最短距離計算することでそれぞれのデータポイントをクラスタリングします。

k-meansクラスタリングでは、セントロイドは、クラスター内の各データポイントの差の総和が最小にするよう更新されます。

k-meansのアルゴリズムは以下の通りに動きます。

Figure1のデータに対してk-meansのアルゴリズムを図示します。

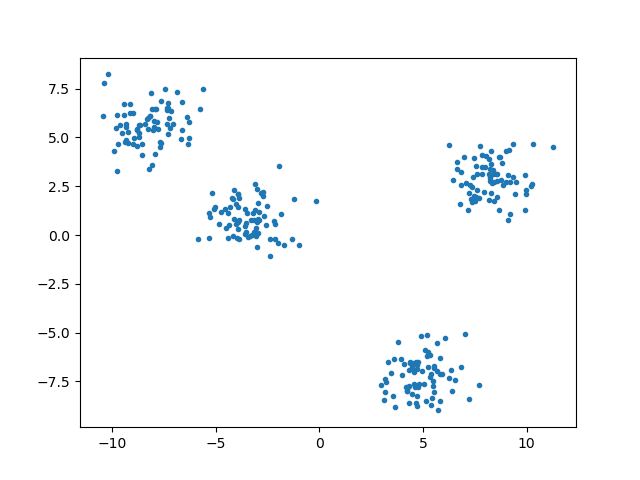
(1)クラスター数の決定：クラスター数を\(k=3\)に設定した場合、ランダムに３点のセントロイドが配置されます。

(2)セントロイドの配置：３つのセントロイドがランダムに配置されます。

(3)クラスターへのアサイン：各データポイントと各セントロイドの距離を計算します。それぞれのデータポイントは、距離が最も近いセントロイドのクラスターにアサインします。

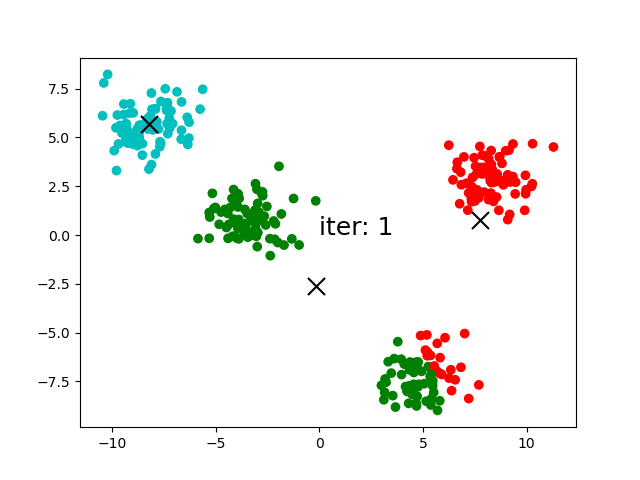
(4)セントロイドの更新：iteration:1でアサインされたクラスター内のデータポイントの座標の平均を新たなセントロイドの座標として更新します。

(5)クラスターの更新：移動したセントロイドとデータポイントの距離の計算し、それぞれのクラスターに含まれるデータポイントを更新します。

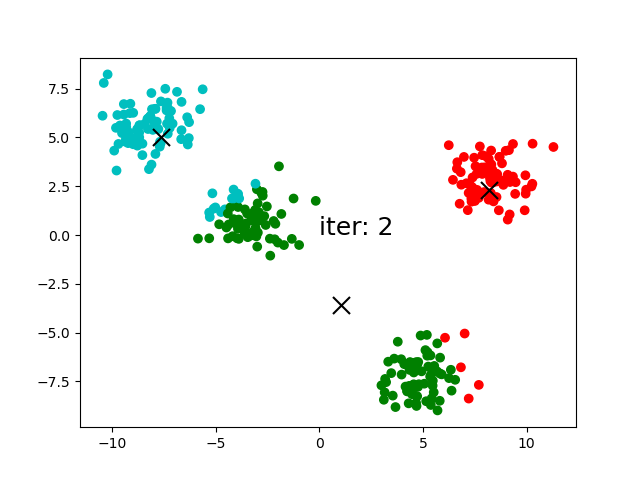
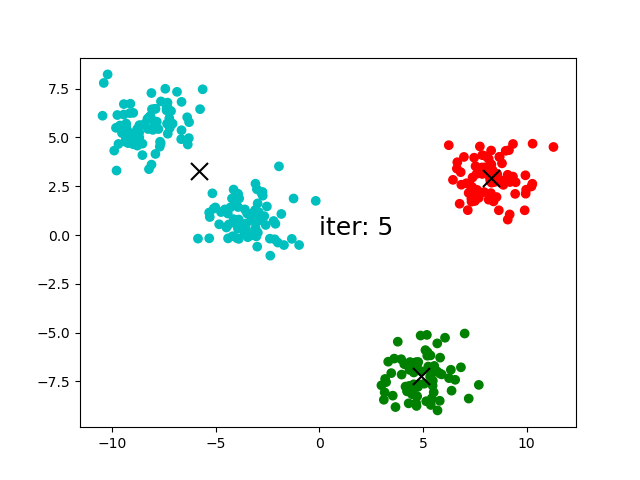
(6)反復：(3)-(5)の操作を継続します。iteration:5以降、セントロイドが移動しなくなりました。

長所と短所

k-meansクラスタリングの長所と短所を教えてください！

ノーフリーランチ定理（No Free Lunch Theorem：NFL)⁽³⁾が「すべての問題に万能に機能するモデルは存在しない」と示すように、あらゆるモデルには長所と短所があります。

ここでは、k-meansクラスタリングの長所と短所をまとめます。⁽⁴⁾

実装が簡単でサイズが大きなデータセットに対しても拡張性が高いk-meansクラスタリングですが、自分でクラスター数を決めなければいけません。

また、セントロイドの位置はランダムに打たれるため、セントロイドの初期値によってクラスタリング結果が変わります。

さらに、k-meansクラスタリングは、セントロイドと各データポイントの距離を基準にグループ化するため、外れ値の影響も受けてしまします。

k-meansクラスタリングに限らず、クラスタリングを扱う際は、それぞれのアルゴリズムの特徴を考慮する必要があります。

教師なし学習に分類されるクラスタリングには絶対的な正解がないことも理由に挙げられます。

アルゴリズムの実装

最後にk-meansのアルゴリズムをPythonで実装します。

クラスター数の決め方

クラスター数:\(k\)を決める方法ってあるんでしょうか？

エルボーメソッドとシルエット分析がk-meansクラスタリングのクラスター数を決める手法として有名です。

エルボーメソッド

エルボーメソッド(Elbow Method)は、k-meansクラスタリングの最適なクラスター数\(k\)を発見する方法です。

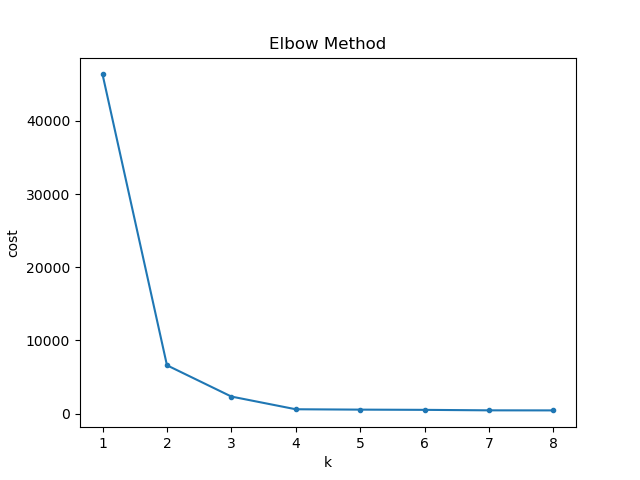
Figure4は、それぞれの\(k\)の値を変えたときのセントロイドとデータポイントの距離の和を示します。

\(k\)の値が\(3\)より大きくなると、傾きが急激に緩やかになっているように見えます。エルボープロットは、勾配が急激に変化する\(k=3\)を最適なクラスター数とみなします。

この線グラフの形がヒジを曲げたように見えることからエルボープロットと呼ばれています。

COST = []
for i in range(1,9):
    kmeans = k_means(k=i, data=X, n_iter=5, centroid_init='random')
    centroids, cluster_assignments = kmeans.fit(X)
    cost = np.sum(cluster_assignments[:,1])
    COST.append(cost)

l = np.arange(1,9)

plt.plot(l,COST,'.-')
plt.xlabel('k')
plt.ylabel('cost')
plt.title('Elbow Method')
plt.show()

シルエット分析

シルエット分析(Silhouette Analysis)は、シルエット係数を計算することでクラスタリングの性能を評価する方法です。

シルエット係数は、(1)クラスター内のデータポイントの凝集度、(2)別クラスターからの乖離度、のふたつを使って計算します。

クラスター\(I: C_I\)に含まれるデータポイント\(i\)において、シルエット係数を\(s(i)\)、凝集度を\(a(i)\)、乖離度を\(b(i)\)とおくと、シルエット係数は

$$s(i)=\frac{b(i)-a(i)}{max(a(i),b(i))}$$

から計算されます。

シルエット係数の値をクラスターごとにソートし、バーグラフにするとFigure5を得ます。このシルエットプロットの結果から、クラスタリングの性能を評価します。

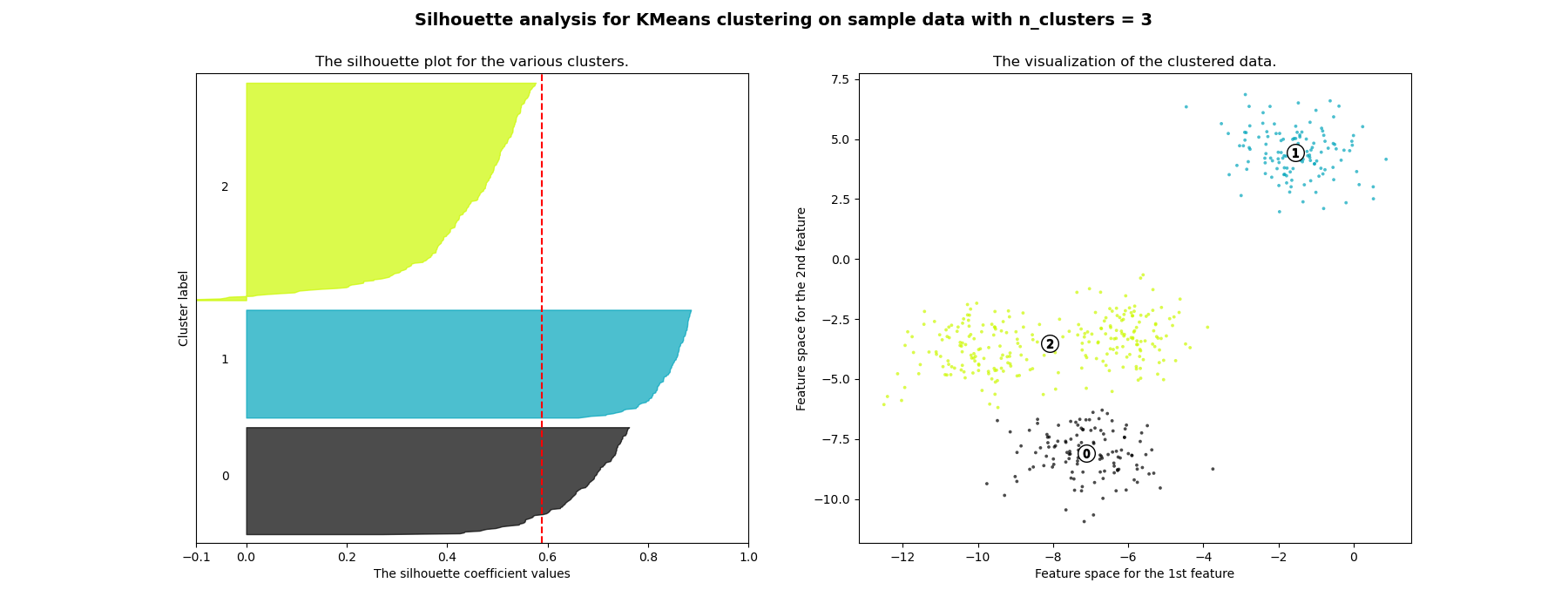
\(k=3\)の場合、クラスター０のシルエットプロットは、平均を下回り、バープロットの幅が広いことから、悪いクラスタリングの例とみなされます。

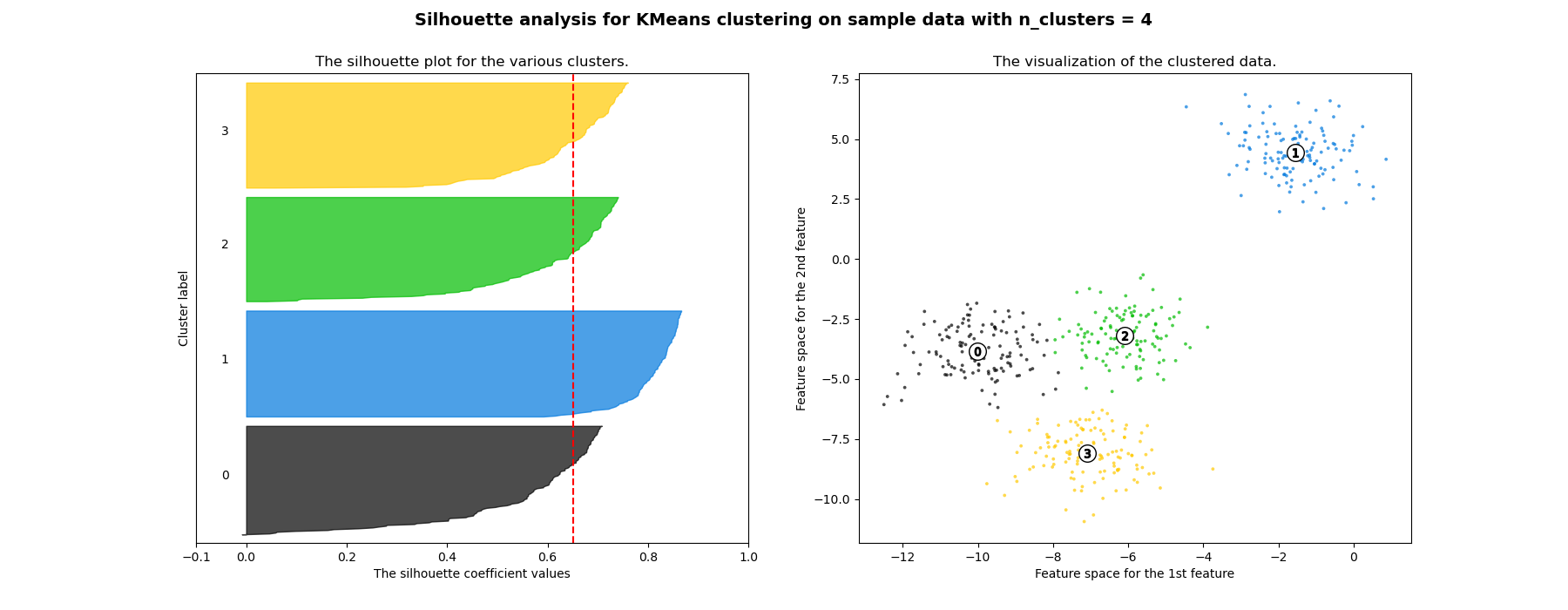
一方、\(k=4\)の場合、すべてのシルエットプロットは平均を上回り、バープロットの幅が均等であることから、良いクラスタリングの例とみなされます。

まとめ

この記事はk-meansクラスターについてまとめました。

k-meansはクラスタリングで必ず紹介される代表的アルゴリズムなので、必ず抑えたいところです。

この記事は以上です。最後まで読んでいただきありがとうございました。

参考資料

(1) Jiawei Han, Micheline Kamber, Jian Pei, Data Mining: Concepts and Techniques, 2: Getting to Know Your Data, 2011

(2) Trevor Hastie, Robert Tibshirani, Jerome Friedman, The Elements of Statistical Learning, Data Mining, Inference, and Prediction, Second Edition, 2017

(3) AI・機械学習の用語辞典、ノーフリーランチ定理（No Free Lunch theorem）とは？(2022/7/3アクセス)

(4) Clustering in Machine Learning, k-Means Advantages and Disadvantages (2022/6/30アクセス)

(5) Scikit-learn, Selecting the number of clusters with silhouette analysis on KMeans clustering (2022/7/4アクセス)