オペレーションズ・リサーチの分野のひとつ「数理計画法」は、数理計画問題(最適化問題)を解くための方法です。
数理計画法は、制約条件を満たし、目的関数を最小、あるいは、最大にする最適解を発見する方法です。数理計画法には様々なアプローチがあり、そのなかのひとつに線形計画法があります。
では、実社会で線形計画法はどのように扱えるのでしょう?
- 線形計画法とは何か
- どうやって例題を数理モデルとして定式化するか
- どうやって定式化した数理モデルをアルゴリズムとして実装するか
線形計画法とは

数理計画法と線形計画法が出てきましたが、両者の違いって具体的に何ですか?
数理計画法 (Mathematical programming)は、現実問題を数理モデルとして定式化し、最適解の取得を試みる方法です。
数理計画法の数理モデルには、
- 目的関数 (Objective function)
- 決定変数 (Decision variables)
- 制約 (Constraints)
を扱います。
決定変数を連続変数として扱う数理計画法は、線形計画法(Linear Programming: LP)に分類されます。
線形計画法は、物流、輸送、製造、農業、エネルギー、をはじめとした様々な分野で利用されます。

このブログのオペレーションズ・リサーチのトピックでは、数理計画法が実社会でどのように利用できるか、いくつか例を紹介していく予定です。
線形計画問題を解いてみよう
例題
大学の講座(チュートリアル)で扱った問題のひとつを使います。今回のお題は、「ある食品会社の利益を最大化するための混合油生産計画」です。(2)
以下が問題文になります。
ある食品会社は、原料油を社外から購入し、自社で原料油を精製している。精製した油は混合し、製品として販売している。製品を作るために植物性油と動物性油を混合している。購入できる植物性油は2種類、非植物性油は3種類ある。1〜6月の期間中の購入コストと生産コストを考慮し、利益を最大化するための生産計画を考えよ。
精製
原料油の精製は、植物性油、動物性油ごとに異なる生産ラインを扱う。1ヶ月あたりに現状の生産ラインで精製できる原料油の最大量は、植物性油が200トン、動物性油が250トンである。今回、精製による質量のロス、精製プロセスのコストは無視する。
硬度
精製した油を使って混合油を製造する。技術的な指標に、油の”硬度”を扱っている。混合油の硬度は3〜6の範囲でなければいけない。混合油の硬度は、組成に含まれる油の加重平均から求められる。各油の硬度は以下のデータで提供されている。
| 油 | Veg1 | Veg2 | Oil1 | Oil2 | Oil3 |
| 硬度 | 8.8 | 6.1 | 2.0 | 4.2 | 5.0 |
購入
原料油は購入後にすぐ調達できる。原料油の購入価格($)は毎月変動する。1月からの6月の価格予想は以下のデータで提供されている。
| 油 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
|---|---|---|---|---|---|---|
| Veg1 | 110 | 130 | 110 | 120 | 100 | 90 |
| Veg2 | 120 | 130 | 140 | 110 | 120 | 110 |
| Oil1 | 130 | 110 | 130 | 120 | 150 | 140 |
| Oil2 | 110 | 90 | 100 | 120 | 110 | 80 |
| Oil3 | 115 | 115 | 95 | 125 | 105 | 135 |
貯蔵
それぞれの原料油は各タンクに最大1000トンまで貯蔵可能である。貯蔵コストは1トンあたり$5かかる。
販売
ブレンド油は、1トンあたり$150で販売する。
現状
現在(1月頭)、タンクにはそれぞれの原料油が500トンずつ貯蔵されている。
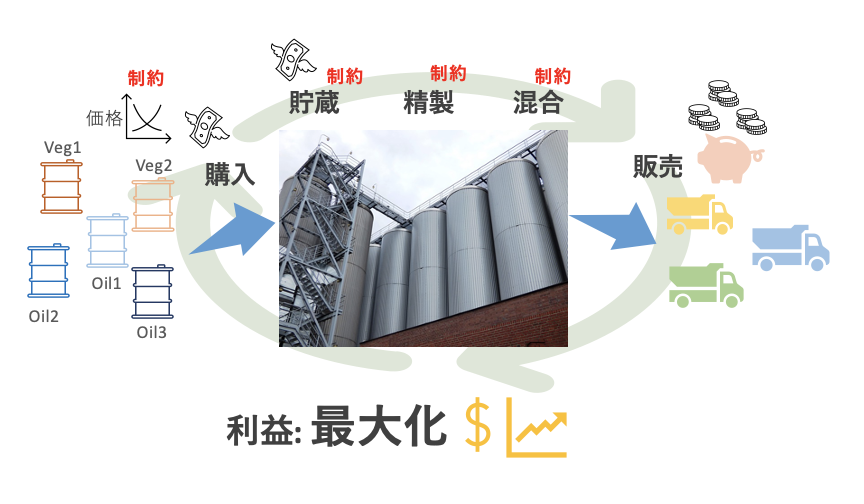
数理モデルの定式化
状況が把握できたら、さっそく問題を数理モデルに定式化してみましょう!
今回の問題に関する「集合」と「データ」を書き出し、「目的関数」「決定変数」「制約」をまとめます。
Sets: 集合
\(I:\) Ingredients 油
\(T:\) month 月
Data: データ
\(cost_{it}:\) 各月の原料油の購入価格 \(i \in I, t \in T\)
\(hard_i:\) 各油の硬度 \(i \in I\)
\(IsVeg_i:\) True: 植物性油, False: 非植物性油 \(i \in I\)
\(Storecost:\) 油1トンあたりの貯蔵コスト
\(StoreMax:\) 各油の最大貯蔵量 \(i \in I\)
\(Init:\) 各油の初期貯蔵量 \(i \in I\)
\(MaxH, MaxMin:\) 混合油の許容硬度の最大値と最小値
\(MaxVeg:\) 植物性油の精製キャパシティ
\(MaxNonVeg:\) 非植物性油の精製キャパシティ
\(Sell:\) 混合油の販売価格
Decision variables: 決定変数
\(x_{it}:\) 製造プロセスで使用する月毎の各油の量 \(i \in I, t \in T\)
\(s_{it}:\) 月末の各油の貯蔵量 \(i \in I, t \in T\)
\(y_{it}:\) 各月で購入する各油の量 \(i \in I, t \in T\)
Objective function: 目的関数→利益の最大化
Constraints: 制約
(1)\(s_{i0} = Init – x_{i0}+y_{i0} \quad \forall i \in I \)
(2)\(s_{it} = s_{i(t-1)} – x_{it}+y_{it} \quad \forall i \in I, t \in T, t > 0 \)
(3)\(\sum_{i \in I} (Hard_i – MinH) x_{it} \geq 0 \quad \forall t \in T \)
(4)\(\sum_{i \in I} (Hard_i – MaxH) x_{it} \leq 0 \quad \forall t \in T\)
(5)\(\sum_{i \in I} x_{it} \leq MaxVeg \quad \forall t \in T\)
(6)\(\sum_{i \in I} x_{it} \leq MaxNonVeg \quad \forall t \in T\)
(7)\(s_{it} \leq StoreMax \quad \forall i \in I, t \in T \)
(8)\(x_{it}, y_{it, }s_{it} \geq 0 \quad \forall i \in I, t \in T \)

数理モデルの\(i \in I\)は、\(i\)が要素、\(I\)が集合です。
\(\forall i \in I\)は、「集合\(I\)の全ての\(i\)について」という意味です。\(\forall \)は、英語で「for all」と読んでます。
制約(1)と制約(2)は、月末の原料油の貯蔵に関する制約です。貯蔵量に対して、製造に利用された量がマイナス、購入した量がプラスに影響します。
制約(3)と制約(4)は、混合油の硬度に関する制約です。硬度を3〜6の範囲に抑えます。
制約(5)、制約(6)は、生産ラインのキャパシティに関する制約です。月に精製できるキャパシティを超えることはできません。
制約(7)は、原料油の貯蔵限界量に関する制約です。
制約(8)は、決定変数に関する制約です。変数は非負です。

あぁぁぁ…、数式見ると頭が痛くなる病が…

今回は線形計画法で何ができるかの雰囲気を掴んでもらえたら大丈夫です!頑張れー!
アルゴリズムの実装
続いて、数理モデルをアルゴリズムに実装します。
1〜63行目までは目的関数、決定変数、制約の実装です。
66行目のm.optimize()は、制約をもとに目的関数を最適化する決定変数を得ます。
69行目以降は、結果確認です。

数理モデルの\(i \in I\)もコンピュータサイエンスの用語に対応すれば、\(i\)をインスタンス、\(I\)をクラスと呼びます。
結果
コードからは以下の結果が得られます。
1月〜6月の間で得られる利益の最大値は、$107,843でした。
それぞれの決定変数の値からは、各月ごとの1)原料油購入量、2)原料油の使用量、3)原料油の貯蔵量、が分かります。
生産、貯蔵量、硬度に関する制約は全て満たしていることが分かります。
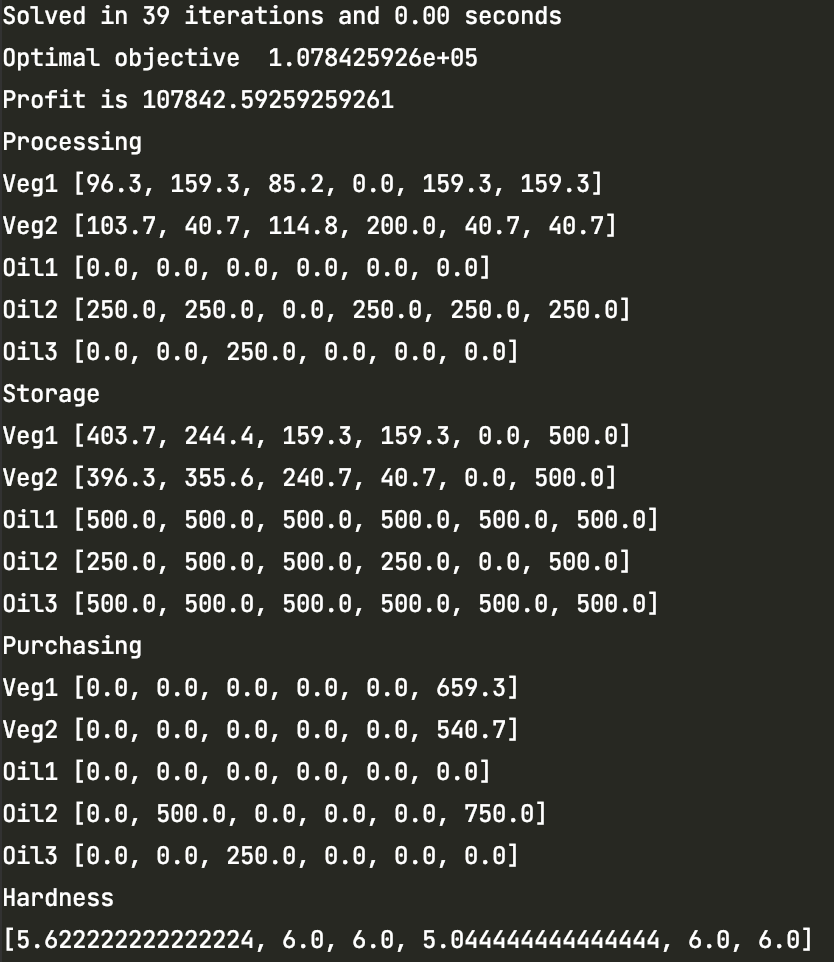
分かりづらい数字だけの結果をグラフにしてみます。
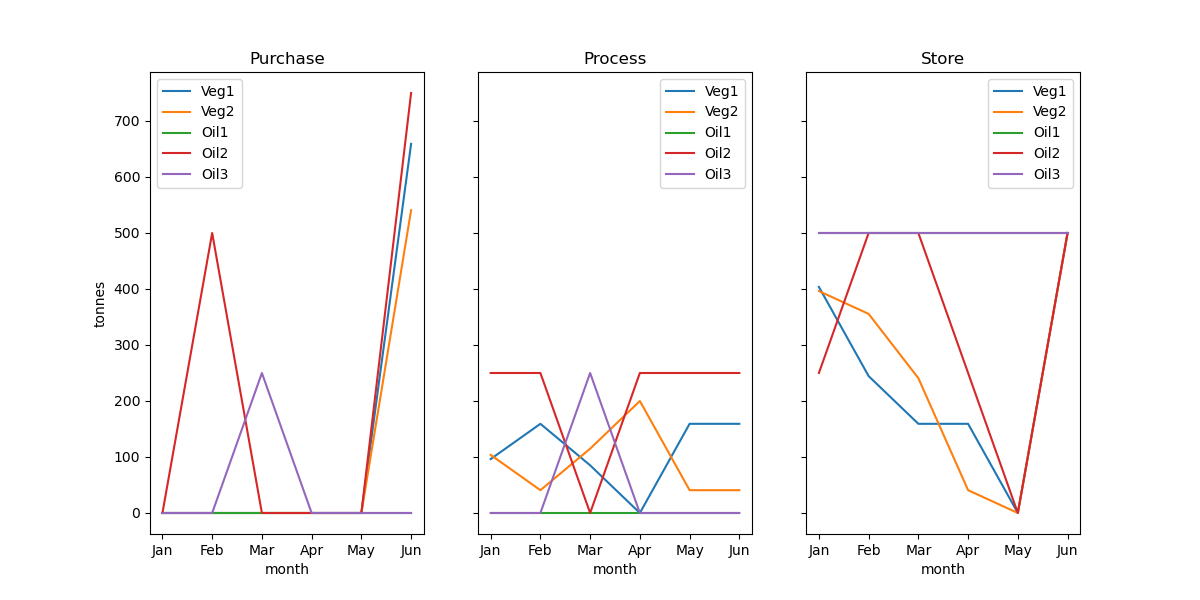

さて、今回の条件から利益を最大化するための原材料購入計画と製造計画が考えられました。ヒトデちゃんなら、この結果のどのポイントに注目し、何を考えますか?

わたしが気になったのは次の3点ですかね。
- Oil1は半年間1度も使用されない
- 5月にVeg1, Veg2, Oil2の在庫量が0になる
- Oil3は製造のために3月に一度使用するのみ。にもかかわらず、Oil3をすぐに購入している。
特に、製造現場のことを考えると、在庫量が0の状況は避けたいです。
そのとおりです。このように、利益を最大化するための最適解が得られても、その答えがビジネスにとって最適な答えとは限らないということです。
今回の結果からだと、
使用しないOil1を貯蔵することに特別な意味があるか?
在庫が0になる前に、原料油を購入する制約を新たに設けるか?
購入を決定するための制約を設ける必要があるか?
といったことが考えられます。

他にも考えたい点があるとすれば、
- 混合油の処方の制約は必要ないのか?
- 毎月製造した製品を全て販売できるのか?
- 混合油は貯蔵しないのか?
- etc…
でしょうか。
今回の例題に対するアルゴリズムから返ってきた利益の最大値は、問題としては正解です。しかし、実務で活用するなら、現場の知識を数理モデルにもっと取り入れる必要があります。
とはいいましても、現実の問題は様々なファクターが関わる複雑な系です。
このように、線形計画法は、あれはどうだ、これはどうだ、といいながら、数理モデルとアルゴリズムの修正を繰り返し、意思決定者に未来のアクションを決断するための情報を提供を目指します。
まとめ
この記事をまとめます。
- 線形計画法:
- 決定変数を連続変数として扱う数理計画法
- 最適解を得るために、目的関数、決定変数、制約を扱う
- 気をつけたい点:
- 得られる最適解が、ビジネスの最適解とは限らない
- 現場とコミュニケーションをしっかりとる

線形計画法のイメージは掴めたでしょうか?基本的には数理計画法の他の流れも同様です。
締まりが悪い説明だったかもしれませんが、線形計画法を含めた数理計画法は、扱えると強力な武器になるだけでなく、現実問題を数学的に捉える訓練にもなります。
ちなみに線形計画法はエクセルでも使えますよ!

おかげさまで数理計画法(線形計画法)の流れがよく分かりました!
以上、線形計画法についてでした。
最後まで読んでいただきありがとうございました。
参考文献
(1): Winston, W. L., & Goldberg, J. B. (2004). Operations research: Applications and algorithms. Belmont, CA: Thomson/Brooks/Cole.
(2): H. Paul Williams, Model Building in Mathematical Programming, 12.1 Food Manufacture, John Wiley & Sons, 2013
(3): Wikipedia, 線型計画法 (7/24/2021アクセス)














この記事では、線形計画法のイメージを掴むことを目的に、線形計画法を使ってある食品会社の生産計画問題を解きます。