クラスタリングは、類似性が高いデータをグループ化する教師なし学習の一種です。
クラスタリングには様々なアルゴリズムがありますが、使用アルゴリズムごとでデータセットから得られる結果も異なります。
さらに、クラスタリングには正解がないため、結果の判断に悩むこともあります。
DBSCAN
概要
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) は、データセットの中から密集しているデータ群を見つけ、クラスタリングする手法です。

なぜDBSCANのような密度ベースクラスタリングが必要になるんでしょう?例えば、k-meansで様々なデータセットに対してクラスタリングすると何が問題になるんでしょう?
例にあげられる分割クラスタリングの一種: k-meansは
- ノイズ/外れ値を含むデータセット
- 「Arbitrary shape」に分類されるデータセット
に対してうまくクラスタリングできないケースが多いです。

Arbitrary shapeとは、以下のようなデータとデータの直線距離間にくぼみ・へこみを持つ集合のことです。Non-convex shapeとも呼ばれます。
k-meansがうまくクラスタリングできない理由の一つに、セントロイドの更新方法があげられます。k-meansは、すべてのデータをいずれかのクラスターにアサインし、クラスター内のデータの座標の平均からクラスターのセントロイド(中心点)を更新・決定するため、k-meansにおいて、ノイズ/外れ値はクラスタリング結果に影響を与えます。
また、k-meansは、最短距離のセントロイドのクラスターにデータをアサインします。そのため、k-meansのような分割クラスタリングは、コンパクトかつ適度に分離された「spherical shape」のデータの集合に対して良いクラスタリング結果を示しますが、窪みやへこみを持つ「arbitrary shape」に対してはうまくクラスタリングできません。(Figure2)
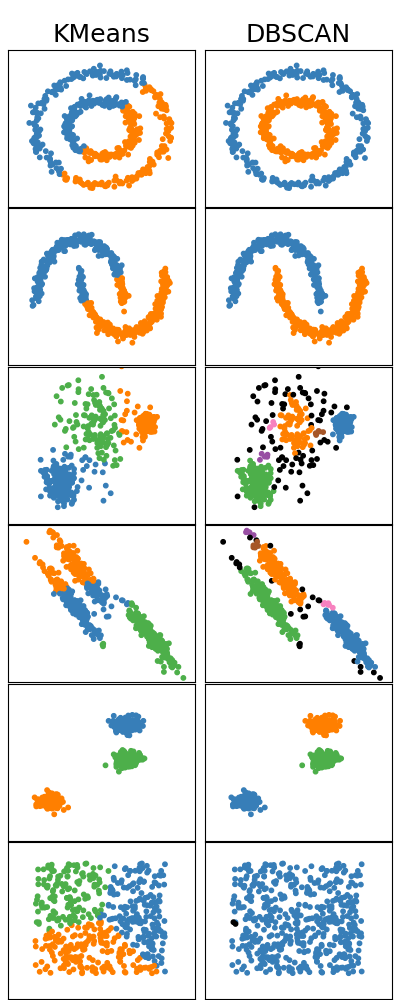
DBSCANのユースケースを以下2点にまとめることができます。
- ノイズ・外れ値を含むデータセット
- Arbitrary shapeに分類されるデータセット
アルゴリズム

DBSCANはどのようなプロセスでクラスターを決定するんでしょう?
まず、DBSCANで扱うパラメーター \(eps\), \(MinPts\)の2つを決定します。2つはデータポイントの密度に関するパラメーターです。
- \(eps\): データポイント\(p\)を中心とした半径の距離。
- \(MinPts\): 半径\(eps\)の内側に含むデータポイントの数の最小値。データポイント\(p\)自身も含む。
続いて、パラメータと以下のアルゴリズムに従ってクラスタリングします。
DBSCANのアルゴリズムを可視化するとFigure3のように動いています。
また、DBSCANではデータポイントはそれぞれ以下の3種に分類されます。

- \(Core point\): \(eps\)の範囲に\(MinPts\)以上のデータポイントを含むデータポイント。
- \(Border point\): \(eps\)の範囲のデータポイントが\(MinPts\)未満、かつ、\(Core point\)を含むデータポイント。
- \(Noise point\): \(eps\)の範囲内のデータポイントが\(MinPts\)未満、かつ、\(Core point\)を含まないデータポイント。

\(Boarder point\)は\(Core point\)から到達可能なデータポイント\(q\)で、\(Core point\)と同じクラスターにアサインされます。
長所と短所
ここでは、DBSCANの長所と短所をまとめます。
Figure5は密度が異なるクラスターの例です。例えば、\(eps\)と\(MinPts\)から密度を高く設定するとcluster3を見落とすかもしれません。逆に、密度を低く設定すると、cluster1とcluster2はマージされてしまいます。


このようなケースでは、DBSCANよりk-meansによるクラスタリングのほうが効果的かもしれません。
epsの決定
k-meansのelbow-methodのように、DBSCANの\(eps\)の決定方法も提案されています。
方法としては、k-nearest neighbour(k=2)でそれぞれのデータポイント\(p\)とデータポイント\(q\)の距離を求め、それをソートして可視化します(Figure6)。
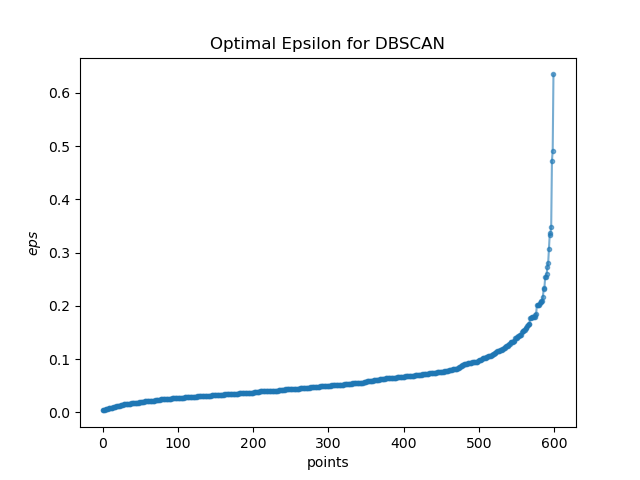
勾配が急上昇し始めるポイントを密度が低いノイズ・外れ値と考えることができます。

このデータを参考にすると、\(eps\):0.15-0.20付近にあたり付けをします。
アルゴリズムの実装
最後にpythonでDBSCANを実装してみます。
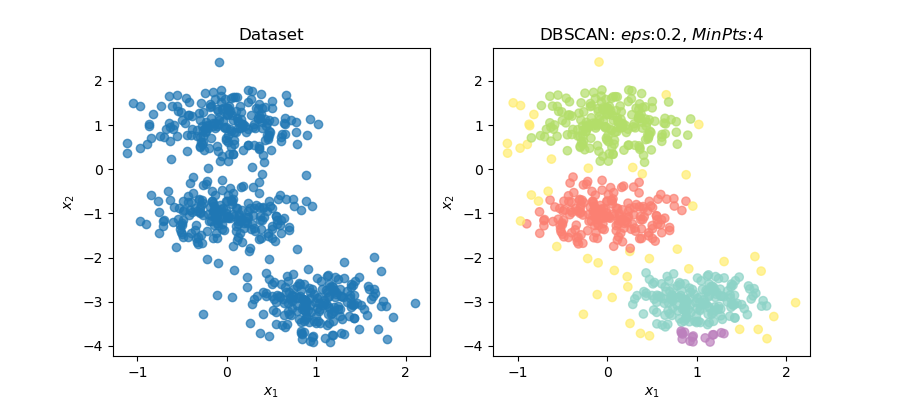
クラスターと外れ値をうまくクラスタリングできていることが確認できました。

DBSCANはsklearn.cluster.DBSCANで扱うことができます。
まとめ
この記事はDBSCANについてまとめました。
- ユースケース
- ノイズ・外れ値を含むデータセット
- Arbitrary shapeに分類されるデータセット
- アルゴリズム
- \(eps\)と\(MinPts\)をパラメーターとして扱う
- パラメーターに従ってコアポイントから到達可能なデータポイントをピックアップし、クラスターを形成
- 長所
- 事前にクラスター数を決定する必要なし
- Arbitrary-shapeと呼ばれる形状のデータに対してよく機能
- 外れ値に対してロバスト
- 短所
- クラスターの密度が異なるケースでの適用 難
- ドメイン知識が必要
- 高次元データに対して「次元の呪い」
この記事は以上です。最後まで読んで頂きありがとうございました。
参考資料
(1) Charu C. Aggarwal, 2015, Data Mining: The Textbook, Springer
(3)Srinivasan, The Top 5 Clustering Algorithms Data Scientists Should Know




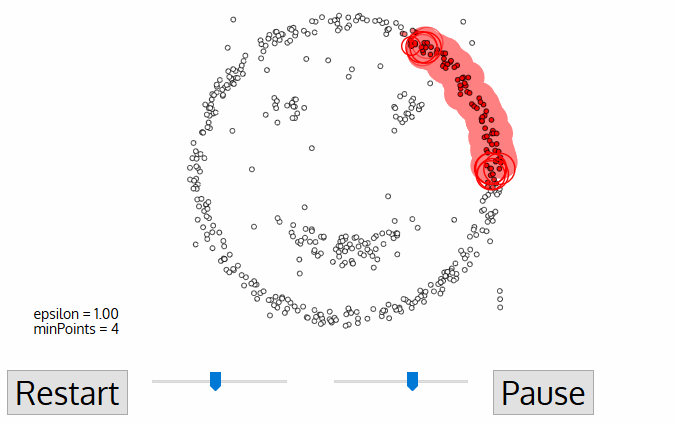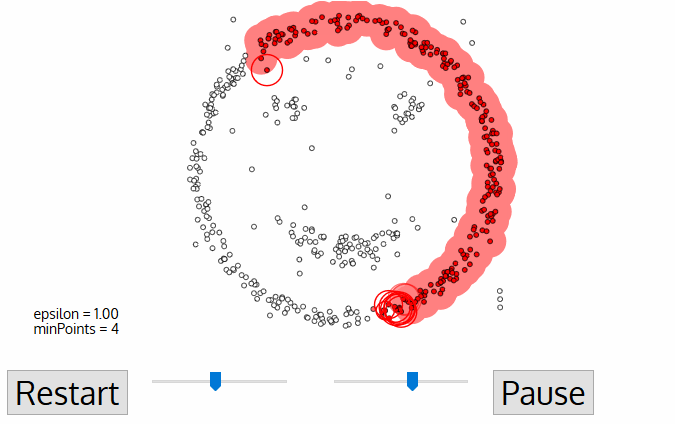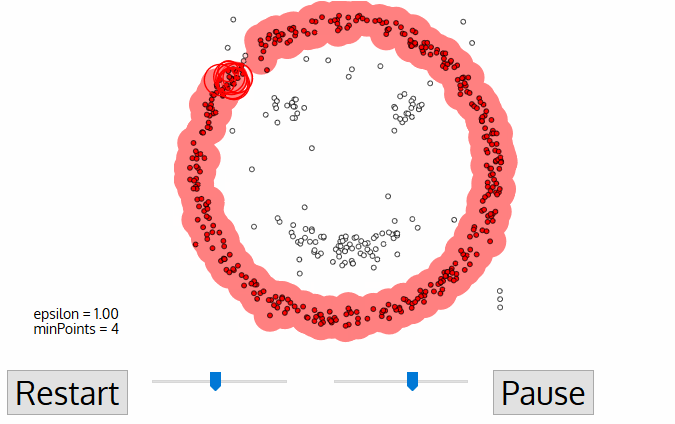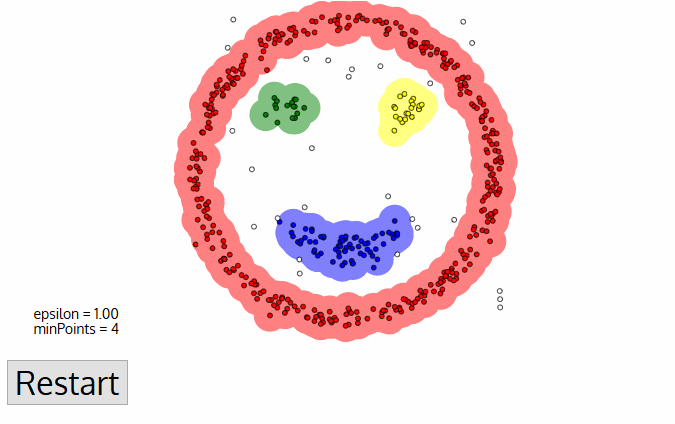














クラスタリングを扱うためには、それぞれのクラスタリングの特徴を把握することは重要とのことで、この記事は、密度ベースクラスタリングの手法のひとつ「DBSCAN」をまとめます。