類似度は、ふたつのオブジェクトがどれくらい似ているかを示します。オブジェクト同士の類似度を計測する方法は、多くのデータマイニング、機械学習の手法で利用されます。
では、どのようにしてオブジェクト同士の類似度を計測するのでしょう?
- どのような類似度計測方法があるか
- それぞれの類似度測定方法の利点・欠点は何か
- どのように類似度の測定方法を使い分けるか
目次
距離と類似性
類似度の計測には「距離ベース」と「類似性ベース」の2つがあります。
- 距離ベース:距離の値が小さければ、オブジェクト同士は類似していると判断します。値が大きいとオブジェクト同士は相違と判断します。代表的な計測方法に、ユークリッド距離、マンハッタン距離、チェビシェフ距離があげられます。
- 類似性ベース:値が1に近づくほど、オブジェクト同士が類似していると判断します。代表的な計測方法に、コサイン類似度、ジャッカード係数、ダイス係数、があげられます。
ドメインによって利用する計測方法は異なります。そして、計測方法が変われば、データの解析結果も変わります。
距離ベースの類似度測定は、座標系を使って位置・意味を表す空間データに対して利用します。
一方、類似性ベースの類似度測定は、テキストデータのような距離を問題としないデータに対して利用します。
距離ベースの類似度計測
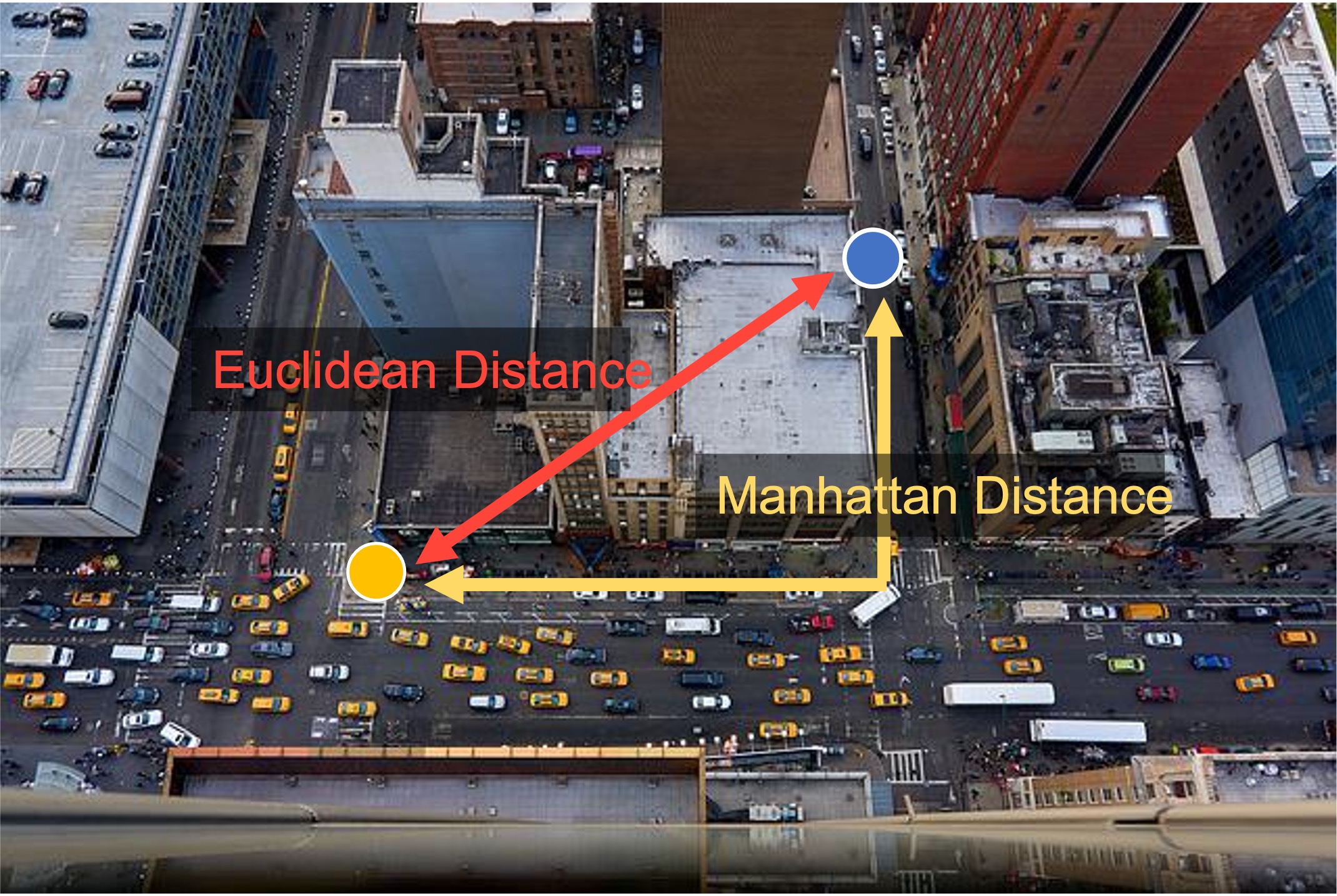
定量データに対して距離を測る関数を「距離関数: Distance function」と呼びます。
2つのオブジェクトをそれぞれ
\(\mathbf{X} = (x_1, \cdots , x_d)\)
\(\mathbf{Y} = (y_1, \cdots , y_d)\)
とおくと、オブジェクト同士の距離は距離関数
$$\textit{Dist}(\mathbf{X},\mathbf{Y})=\left(\sum_{i=1}^{d}|x_i-y_i|^p\right)^{1/p}$$
から計算できます。
この距離関数を\(L_p\)ノルムと呼び、定量データの類似度の計測に利用されます。
単位の違いの影響を回避するため、距離関数を用いる前に正規化(Normalization)の実施が勧められます。
Euclidean Distance: ユークリッド距離
距離関数: \(L_p\)ノルムが\(p=2\)のとき、ユークリッド距離(または\(L_2\)ノルム)と呼びます。
このとき、オブジェクト同士の距離は
$$\textit{Dist}(\mathbf{X},\mathbf{Y})=\sqrt{ \sum_{i=1}^{d}(x_i-y_i)^2 }$$
と定義されます。
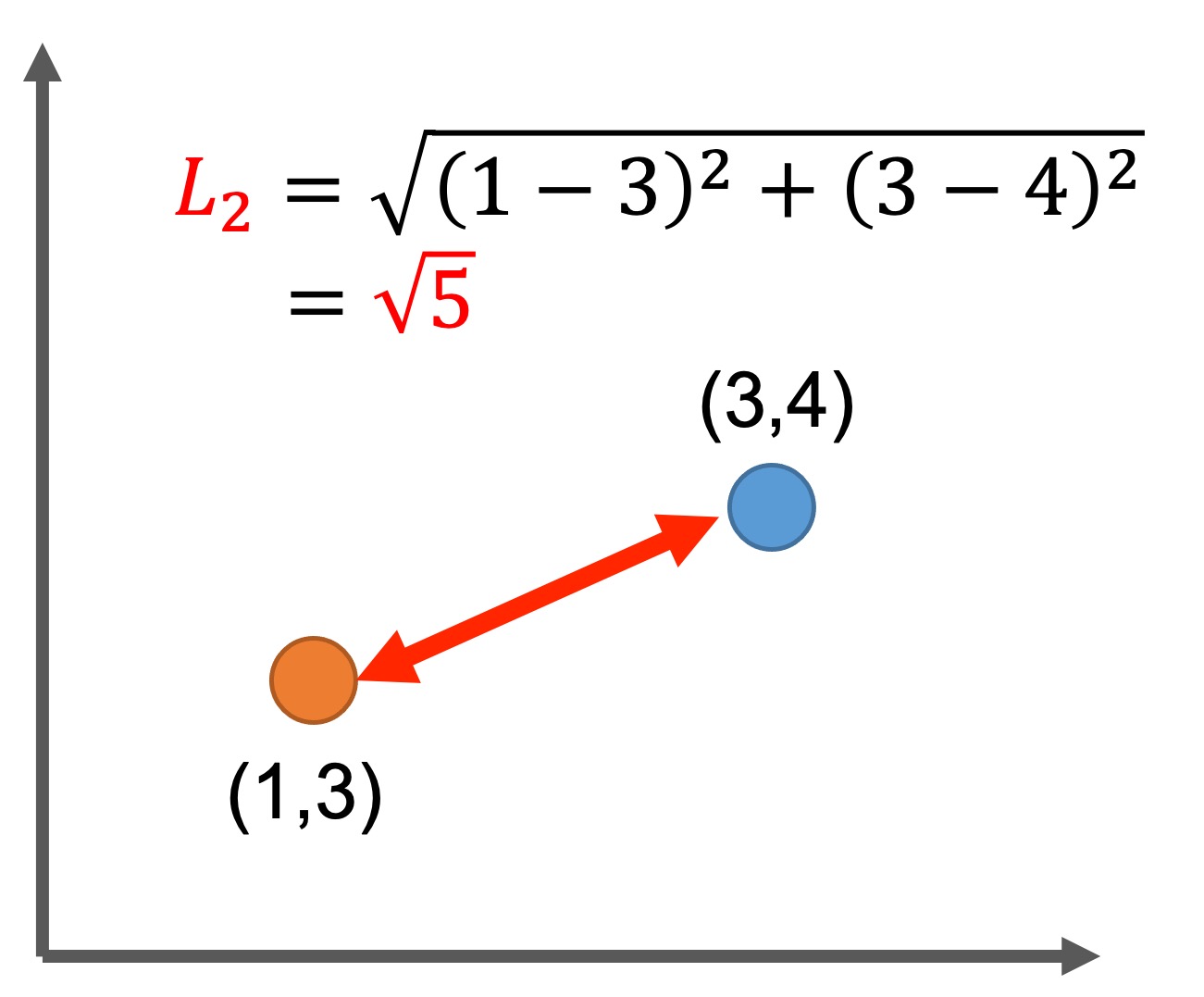
距離ベースの類似度計測において、ユークリッド距離は頻繁に利用されます。ユークリッド距離は、ユークリッド幾何学におけるオブジェクト間の最短直線距離として捉えます。
ユークリッド距離は、回転に対して影響を受けない性質(回転不変)を持ち、座標軸が回転してもオブジェクト間の距離は変わりません。
一方、ユークリッド距離を含む距離ベースの類似度計測は、高次元になるに従って「次元の呪い」の影響を受け、距離の本質的意味が失われます。その結果、クラスタリング、分類、異常検知のアルゴリズムの性能が低下します。
Manhattan Distance: マンハッタン距離
距離関数: \(L_p\)ノルムが\(p=1\)のとき、マンハッタン距離(または\(L_1\)ノルム)と呼びます。
このとき、オブジェクト同士の距離は
$$\textit{Dist}(\mathbf{X},\mathbf{Y})=\sum_{i=1}^{d}|x_i-y_i|$$
と定義されます。
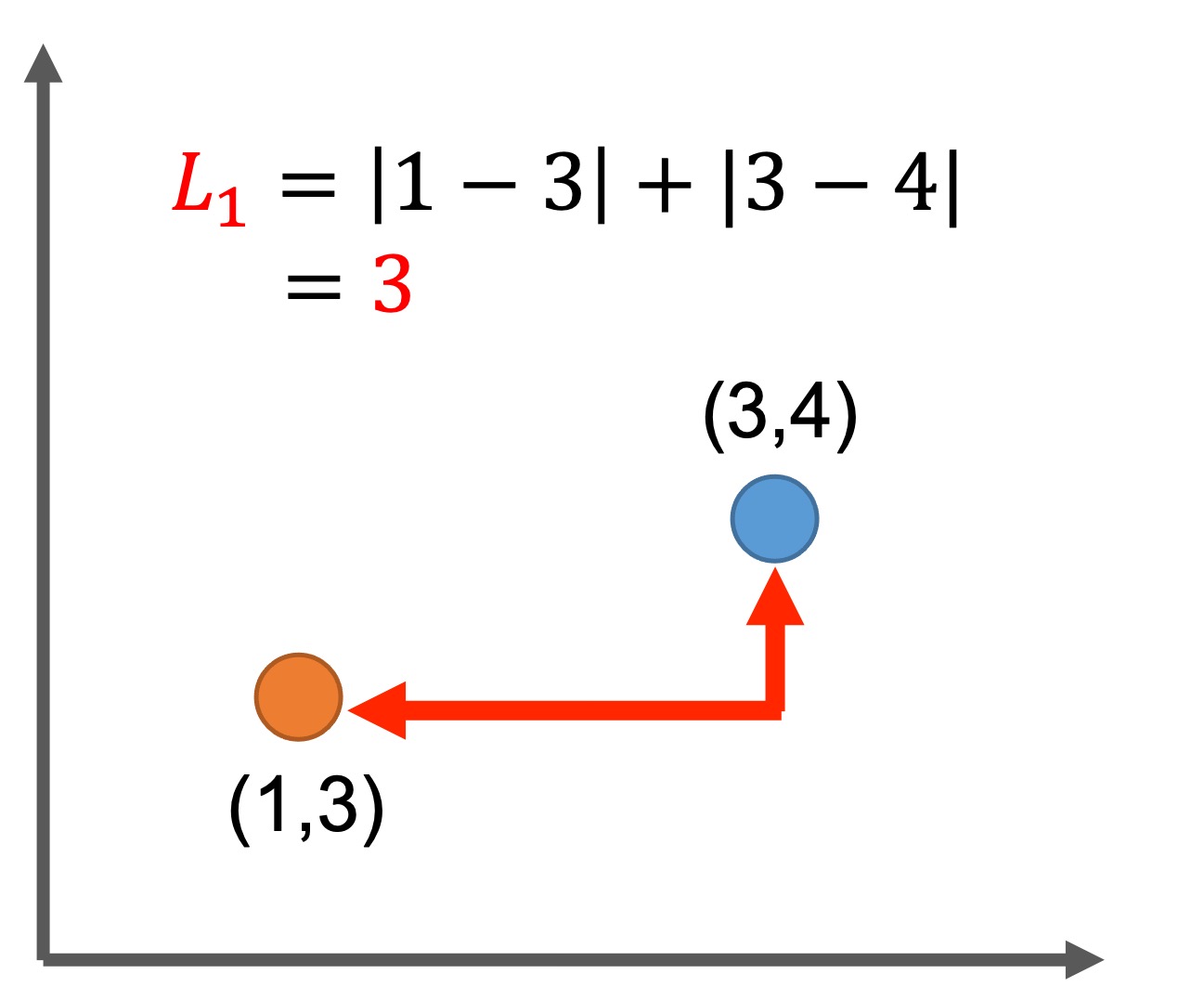
マンハッタン距離は、ニューヨーク・シティのマンハッタン島のように整備された区画ブロックを走るタクシーになぞらえ、シティ・ブロック距離と呼ばれることもあります。
マンハッタン距離は、ユークリッド距離に比べて外れ値の影響を小さくします。オブジェクト間の差を二乗しないためです。
マンハッタン距離は、高次元データの場合、クラスタリングのようなモデルの性能を向上するにはユークリッド距離より好ましい傾向にあると報告されています。(3)
Chebyshev Distance: チェビシェフ距離
距離関数: \(L_p\)ノルムが\(p=\infty\)のとき、チェビシェフ距離(または\(L_\infty\)ノルム)と呼びます。
このとき、オブジェクト同士の距離は
$$\textit{Dist}(\mathbf{X},\mathbf{Y})=\max_{i} |x_i-y_i|$$
と定義されます。
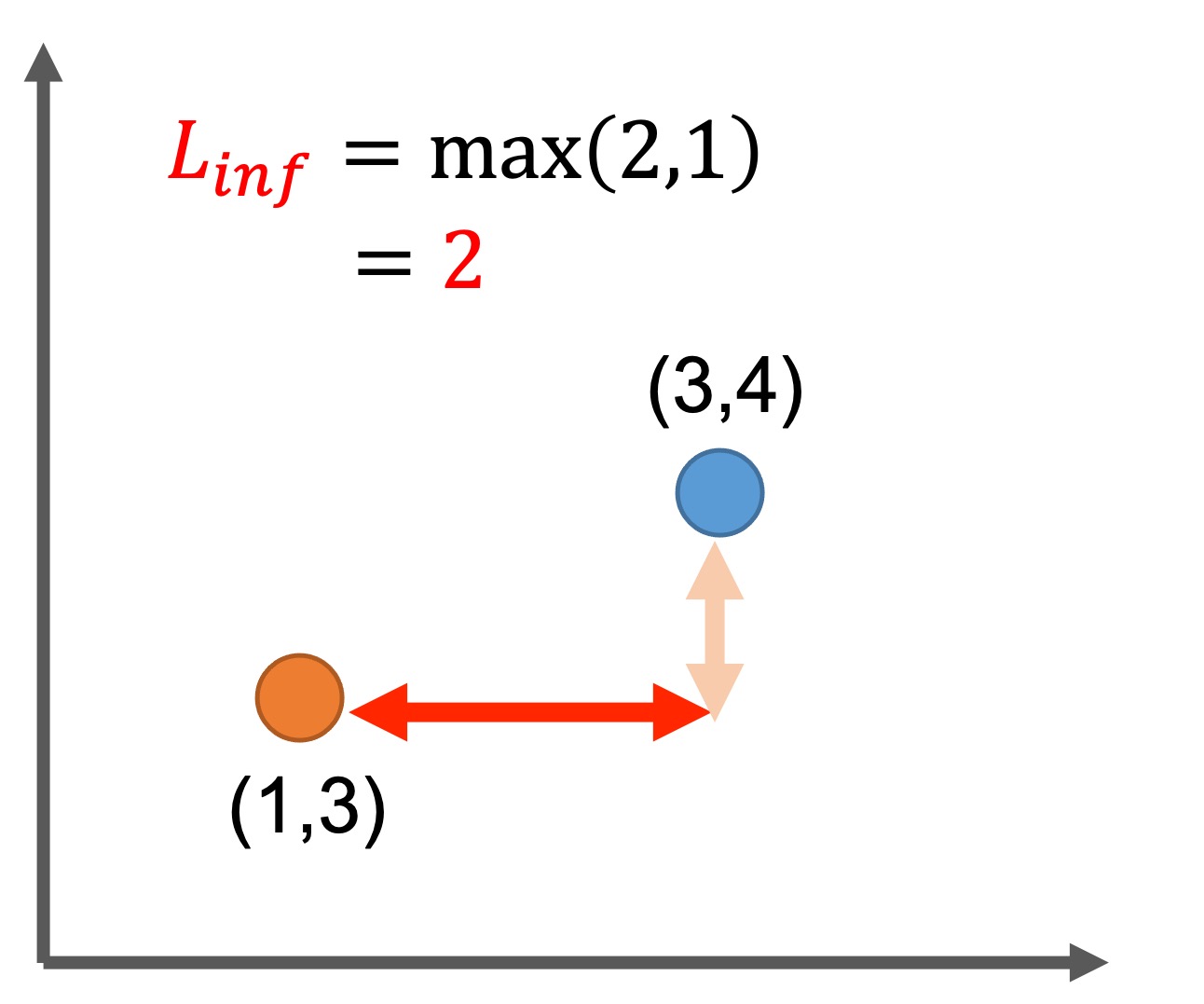
チェビシェフ距離は、絶対値が最大にならない要素の距離は切り捨てます。重要ではない小さなノイズを除去するために利用します。
一つの要素だけで距離を決定するため、全体としての距離を測定できないことが欠点にあげられます。
チェビシェフ距離は特殊なケースで利用されることが多く、例として、オーバークレーンが荷物を運ぶ時間を計測する倉庫のロジスティクスが挙げられるそうです。(4)
比較

成績のデータを例に、それぞれの計測方法を比較してみます。
下記方法で評価を実施しました。
- 生徒Xと生徒Yの成績データ10科目を生成。
- 次元を1から10まで変化させ、それぞれの距離関数を使って距離を計算。
import numpy as np
import matplotlib.pyplot as plt
# data object
np.random.seed(123)
X = np.random.randint(50,100,size=10)
Y = np.random.randint(50,100,size=10)
# dimension
P = np.arange(1,11)
# list
L1s = []
L2s = []
Linfs = []
for p in P:
# set features
X_dim = X[:p]
Y_dim = Y[:p]
# compute distance
L1 = sum(abs(X_dim-Y_dim))
L2 = np.sqrt(sum(np.power((X_dim-Y_dim),2)))
Linf = np.max(abs(X_dim-Y_dim))
# save result
L1s.append(L1)
L2s.append(L2)
Linfs.append(Linf)
# visualization
plt.plot(P,L1s,'.-',label='Manhattan')
plt.plot(P,L2s,'.-',label='Euclidean')
plt.plot(P,Linfs,'.-',label='Chebyshev')
plt.ylabel(r'$Dist (X,Y)$')
plt.xlabel(r'$p:Dimension$')
plt.legend()
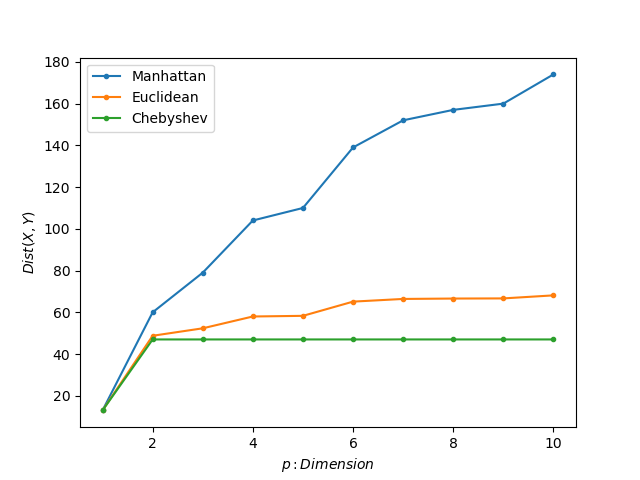
plt.show()Figure4は結果になります。興味深いことにマンハッタン距離は値が上昇し続けています。一方、ユークリッド距離は、\(p=6\)以降から収束し始めているように見えます。また、チェビシェフ距離は\(p=2\)が最大の差だったようで、次元が増えても値の変化は見られませんでした。
教科数500の試験と仮定した高次元のデータを作り、同じ評価をしてみました。(例えが悪いか…)
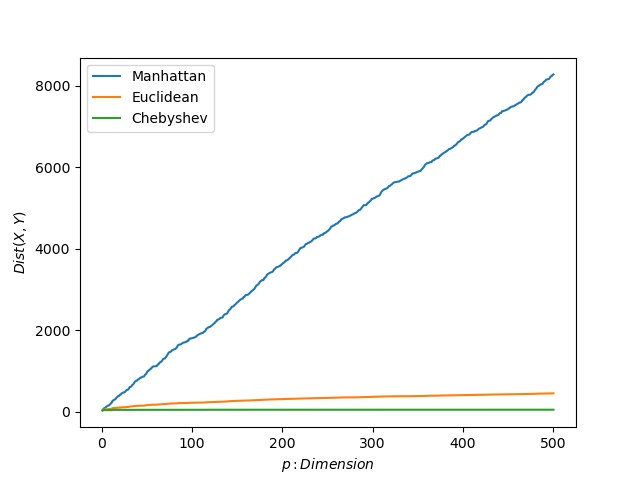
マンハッタン距離の値は比例的に上昇しています。一方、ユークリッド距離とチェビシェフ距離の値はマンハッタン距離と比較して変化が非常に小さいということが分かりました。(収束している)

同じデータでも扱う距離関数によって得られる値や挙動が異なるんですね。
類似性ベースの類似度計測
高次元となるドメインのデータに対して、類似性ベースの類似度計測が利用されます。類似度を測定する関数を「類似度関数: Similarity function」と呼びます。
ここでは、コサイン類似度、ジャッカード係数、ダイス係数についてまとめます。
Cosine Similarity: コサイン類似度
コサイン類似度は、2つのベクトルの角度を使って類似度を計測します。
類似度関数を\(\textit{Sim}(\mathbf{\cdot},\mathbf{\cdot})\)とおくと
このとき、オブジェクト同士の類似度は
$$\textit{Sim}(\mathbf{X},\mathbf{Y})=\frac{\mathbf{X}\cdot \mathbf{Y}}{\| \mathbf{X} \| \| \mathbf{Y} \|}$$
と定義されます。
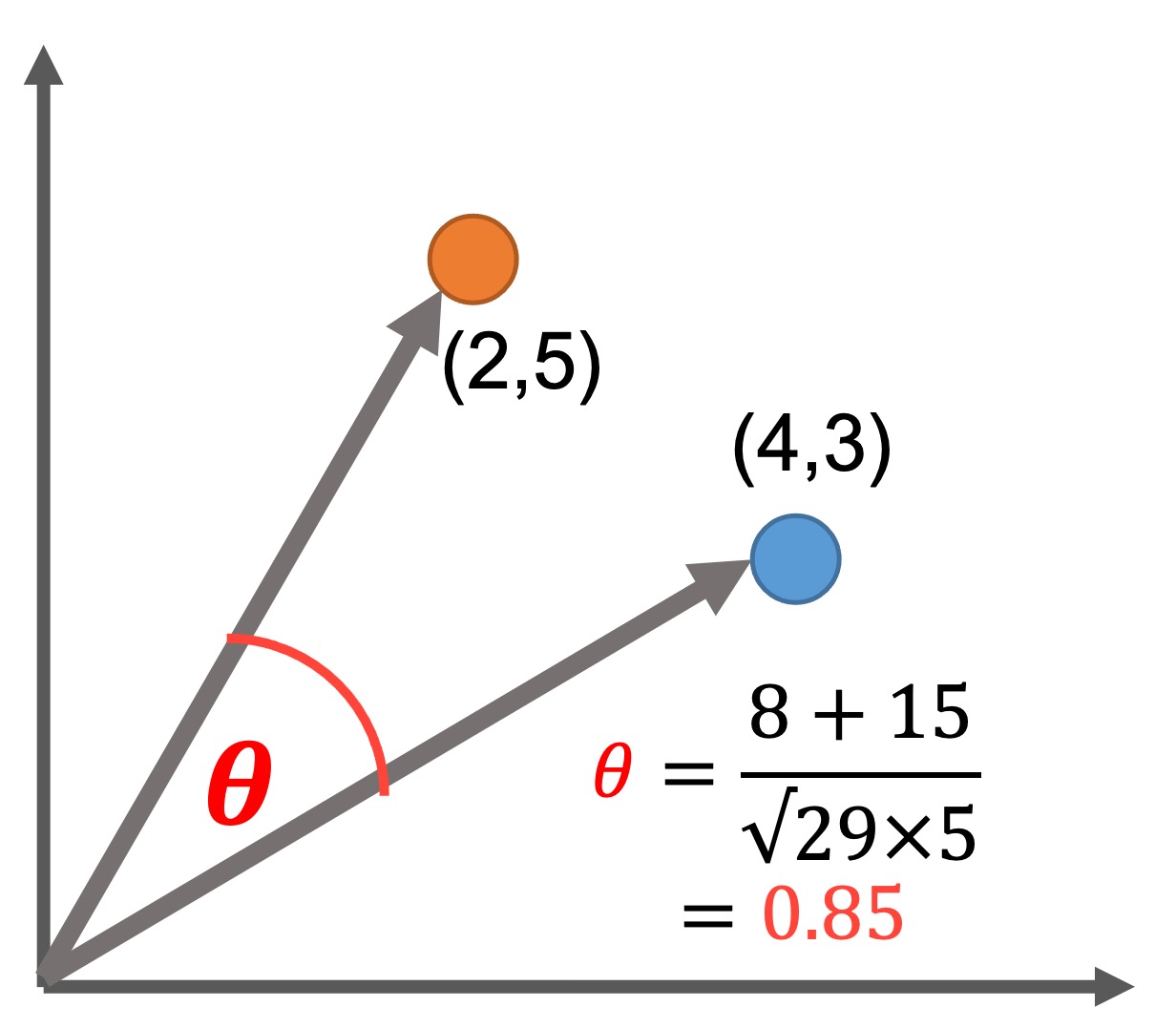
コサイン類似度は、ベクトルの大きさを重要視しない次元が大きなデータに対して利用します。オブジェクト同士が似ていれば、値は1に近づきます。一方、オブジェクト同士が全く似ていなければ、値は−1に近づきます。
注意点としては、コサイン類似度はベクトルの大きさを問題としておらず、方向性に注目していることです。
import numpy as np
def cos_sim(X,Y):
return np.dot(X,Y)/(np.linalg.norm(X)*np.linalg.norm(Y))
X = np.array([2,5])
Y = np.array([4,3])
cos_sim(X,Y)Jaccard Similarity Coefficient: ジャッカード係数
ジャッカード係数は、2つの集合の共通要素の割合から類似度を計測します。このとき類似度は、
$$\textit{Sim}(A,B)=\frac{|A\cap B|}{| A \cup B |}$$
集合Aと集合Bが共通部分を多く持つにしたがって、値は1に近づきます。
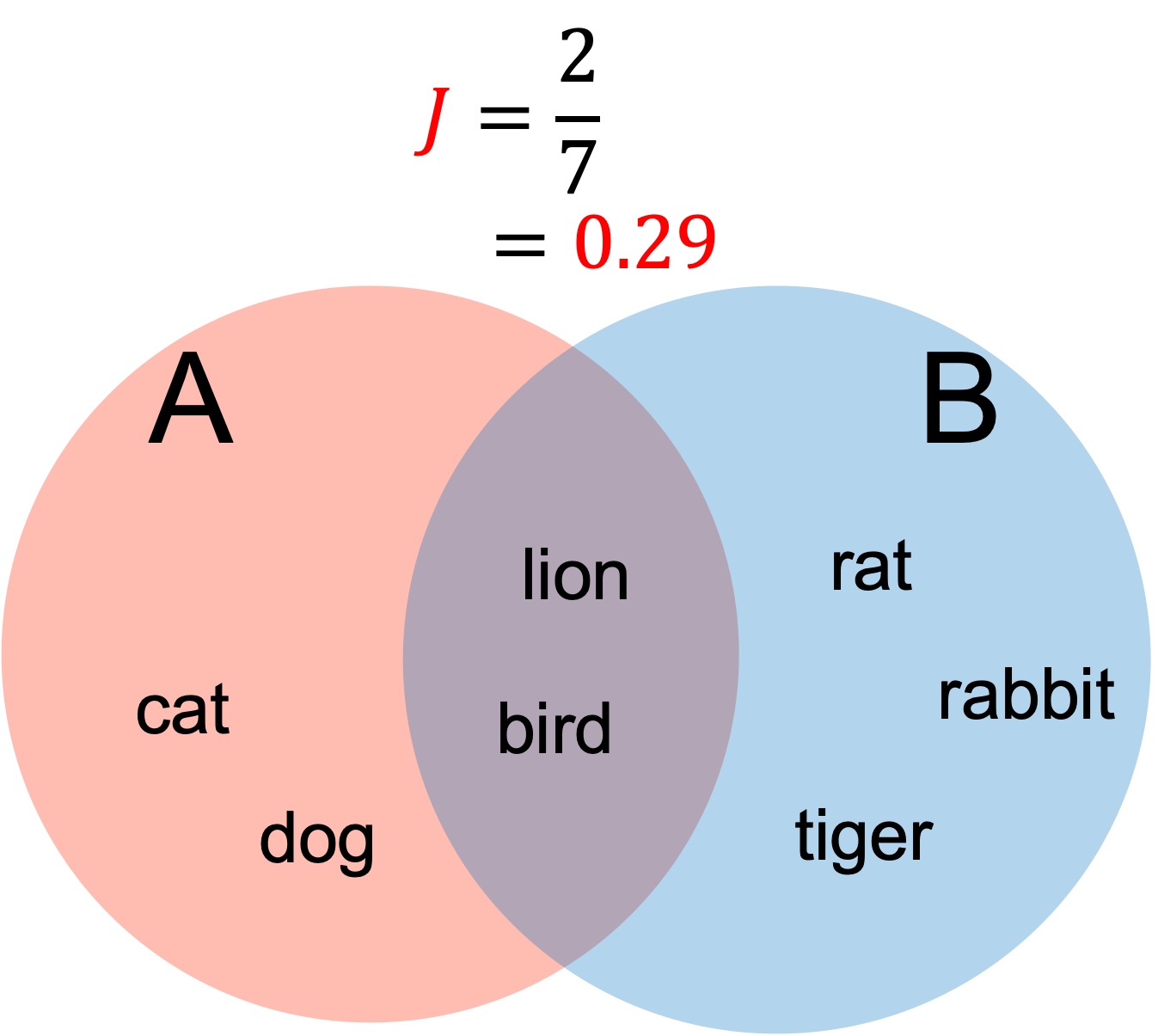
ジャッカード係数は、テキストマイニング、イメージセグメンテーション、共起ネットワーク分析などで利用されます。
欠点として、集合のサイズがあげられます。一方の集合に含まれる要素の数が増えると分母(和集合)が大きくなるため、共通要素の影響、つまり、ジャッカード係数の値が小さくなってしまいます。
import numpy as np
def jaccard_sim(A,B):
return len(np.intersect1d(A,B))/len(np.union1d(A,B))
A = ['cat','dog','lion','bird']
B = ['lion','bird','rabbit','rat','tiger']
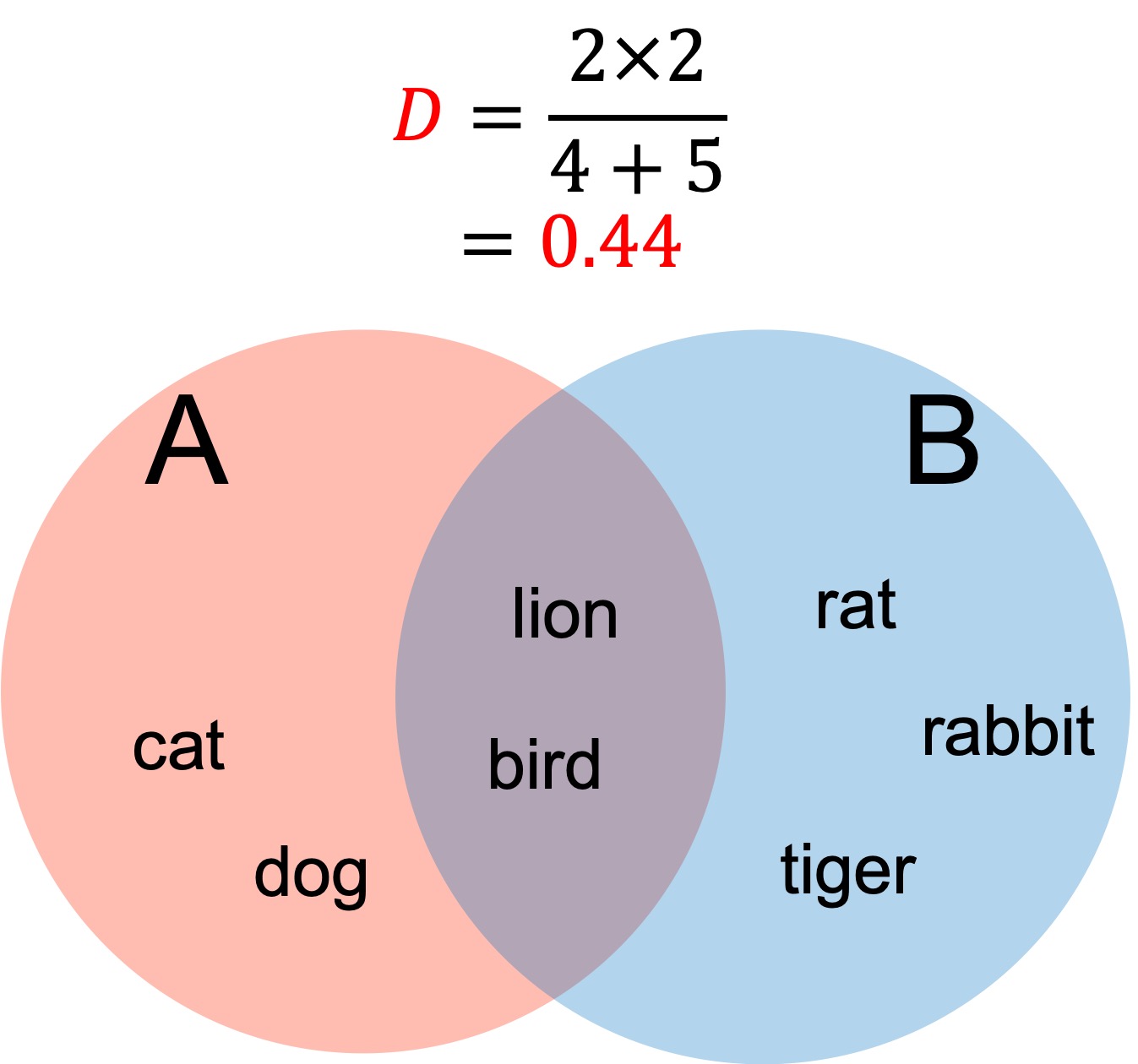
jaccard_sim(A,B)Dice Similarity Coefficient: ダイス係数
ダイス係数は、ジャッカード係数とよく似た類似度計測方法です。ダイス係数は
$$\textit{Sim}(A,B)=\frac{2|A\cap B|}{|A|+|B|}$$
から類似度を計測します。
集合Aと集合Bが共通部分を多く持つにしたがって、値は1に近づきます。
ダイス係数は、ジャッカード係数同様、テキストマイニング、イメージセグメンテーション、共起ネットワーク分析などで利用されます。
ダイス係数は、共通要素にウェイトをかけることで、共通要素の影響を増大させています。しかしながら、ジャッカード係数同様、一方の集合の要素数が大きくなれば、類似度は小さくなってしまいます。
import numpy as np
def dice_sim(A,B):
return 2*len(np.intersect1d(A,B))/(len(A)+len(B))
A = ['cat','dog','lion','bird']
B = ['lion','bird','rabbit','rat','tiger']
dice_sim(A,B)まとめ
この記事は類似度計測の手法についてまとめました。
- 類似度計測は大きく分けて「距離ベース」「類似性ベース」の2種類
- 距離ベース
- 座標系を使って位置・意味を表す空間データに利用
- ユークリッド距離:オブジェクト間の最短直線距離を距離と捉える
- マンハッタン距離:全ての要素の和を距離と捉える
- チェビシェフ距離:全要素の中で最大となる要素を距離と捉える
- 距離ベースの類似度計測は、高次元になるに従って「次元の呪い」の影響を受ける。クラスタリング、分類、異常検知のアルゴリズムの性能が低下。
- 類似性ベース
- ベクトルの大きさを重要視しないデータに利用
- コサイン類似度:ベクトルの大きさを問題とせず、方向性を基準とした類似度測定
- ジャッカード係数、ダイス係数:共通要素を用いた類似度測定

今回は代表的な手法をまとめましたが、類似度計測はさまざまな種類があります。また、どの方法がベストというものはなく、目的に合わせて手法を使い分けなければいけない点はなかなか難しく、経験と知識に勝るのはないと感じる次第でした。
この記事は以上です。最後まで読んで頂きありがとうございました!
参考資料
(1) Jiawei Han, Micheline Kamber, Jian Pei, Data Mining: Concepts and Techniques, 2: Getting to Know Your Data, 2011
(2) Maarten Grootendorst, Toward Data Science, “9 Distance Measures in Data Science”, Feb 1 2021
(4) Wikipedia, Chebysev distance

















この記事は「類似度の計測手法」についてまとめます。