オペレーションズ・リサーチの分野のひとつである「数理計画法」は、数理計画問題(最適化問題)を解くための方法です。数理計画法の様々なアプローチのうちのひとつに「整数計画法」があります。
- 整数計画法とは何か
- どうやって例題を数理モデルとして定式化するか
- どうやって定式化した数理モデルをアルゴリズムとして実装するか
整数計画法

整数計画法はどんな方法ですか?
決定変数を整数として扱う数理計画法を「整数計画法(Integer Programming: IP)」と呼びます。
整数計画法は、
- 純粋整数計画法(pure integer programming): 決定変数を全て整数として問題を解く方法
- 混合整数計画法(mixed integer programming): 決定変数の一部を整数として問題を解く方法
- 0-1整数計問題(zero-one integer programming): 決定変数が0または1のみに限定して問題を解く方法
とさらに細かく分類されます。(1)
整数計画法は、「変数が整数」という制約を線形計画法に追加した方法と捉えることができます。整数計画法で扱う関数と変数は、線形計画法と同様です。
- 目的関数 (Objective function)
- 決定変数 (Decision variables)
- 制約 (Constraints)
なぜ整数計画法は難しい?

「整数計画法は線形計画法より難くなる」と聞きますが、なぜでしょう?
計算機で解く問題の困難さを考える計算量理論において、線形計画法(LP)はP、一方、整数計画法(IP)はNP-hardだからです。(2)

???
線形計画法は、実行可能領域の端点に注目して最適解を決定します。実行可能領域は多面体です。そして、目的関数の最大・最小値は、多面体の端点で達成されます。多面体のある端点が、線形計画問題の最適解になります。
一方、整数計画法は、線形計画法に「決定変数は整数である」という制約を加えています。しかし、実行可能領域の端点が必ず整数とは限りません。そのため、整数計画法は、端点に注目するだけでは最適解を得られません。整数計画法は、実行可能領域中に含まれるたくさんの整数の組み合わせのトライ&エラーから最適解を決定します。

これが、整数計画法が線形計画法より難しくなると言われるポイントです。

確かに全部の組み合わせを試せって言われると大変そうです。
ところで、P、NPって何ですか?
この記事では説明を割愛しますが、P、NPは、計算量理論におけるクラスです。
- P(Polynomial Time):多項式時間内で解ける判定問題のクラス
- NP(Non-deterministic-polynomial Time):答えが”yes”となるような問いに対して、多項式時間で検証できる証拠が存在する判定問題のクラス
です。
参考までに「ソフトウェアサイエンスの基本 シリーズ第3回 計算複雑さの研究って?」のリンクを貼っておきます。(3)

ちなみに「P≠NP予想」という問題は2021年時点でも解決できておらず、クレイ研究所のミレニアム問題になっています。(4) 証明できると懸賞金100万ドルだそうです。
整数計画法を使って問題を解いてみよう
例題
今回のお題は「新しい工場の建設計画」です。
ある会社は新製品を開発した。この製品を20社の大口顧客へ供給するため、工場の建設計画を立てている。現在、10拠点が工場の建設候補地にあげられている。現在、コストに関して、「工場の建設コスト」と「工場から顧客への製品配送コスト」があげられている。工場の建設と製品の配送コストの合計を最小化するための建設計画を考えよ。
顧客と工場
各顧客はどれか1つの工場から製品を受け取る。
工場のキャパシティ
ひとつの工場が受け入れられる顧客の数は最大6である。
オプション
会社には、大きな工場を建設するという選択肢もある。大きな工場を建設した場合、標準工場の建設コストの50%を建設コストに上乗せする必要がある、工場が受け入れられる顧客の数は最大8までになる。
数理モデルの定式化
続いて、問題を数理モデルに定式化します。
今回の問題に関する「集合」と「データ」を書き出し、「目的関数」「決定変数」「制約」をまとめます。
Sets: 集合
\(F: \) Factory locations 工場の建設予定地
\(C: \) Customers 顧客
Data: データ
\(build_{f}: \) 工場の建設コスト \(f \in F\)
\(cost_{c,f}: \) 工場から顧客への製品輸送コスト \(c \in C, f \in F\)
\(maxcap: \) 工場が顧客を受け入れられるキャパシティ
\(add: \) オプションを選択した工場の顧客受入増加数
Decision Variable: 決定変数
\(x_{f}: \) バイナリ変数: 工場を建設する場合1、しない場合0 \(f \in F\)
\(y_{c,f}: \) バイナリ変数: 工場から顧客へ輸送する場合1、しない場合0 \(c \in C, f \in F\)
\(z_{f}: \) バイナリ変数: 工場がオプションを選択する場合1、しない場合0 \(f \in F\)
Objective Funcition: 目的関数→コストの最小化
Constraints: 制約
(1)\(\sum_{f \in F} y_{c,f} = 1 \quad \forall c \in C\)
(2)\(\sum_{c \in C} y_{c,f} \leq maxcap \times x_f + add \times z_f \quad \forall f \in F\)
(3)\(z_f \leq x_f \quad \forall f \in F\)

扱う決定変数が全てバイナリ変数だから、この問題は0-1整数計問題ということですね!
制約に関して、(1)は、顧客と工場の関係に関する制約です。顧客は必ずどこかひとつ工場から製品を受け取ります。
(2)は、工場が受け入れられる顧客の数に関する制約です。大きな工場を建設した場合、その工場のキャパシティは\(add\)だけ増加します。
(3)は、オプションに関する制約です。オプションは建設予定地の工場だけに対して選択できます。
アルゴリズムの実装

ここでは、上の数理モデルをアルゴリズムとして実装します。データの値はランダムに決めました。
m.addVar(vtype=GRB.BINARY)から決定変数のタイプを決めることができます。Gurobiが扱う変数の種類については「GUROBI OPTIMIZATION: Variables」にて。
では、このコードを実行するとどうなるでしょう。
結果
先ほどのアルゴリズムから、以下の結果が得られます。
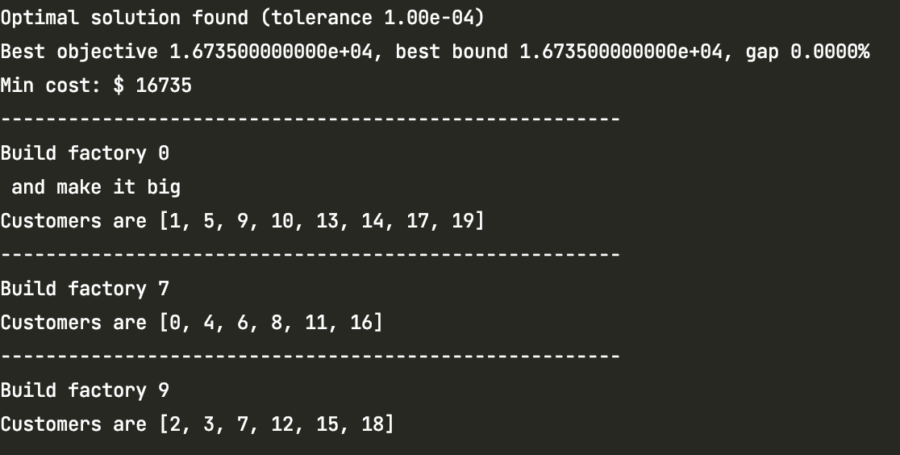
現在把握している条件から得られる総コストの最小値は$16,735です。
このコストを達成するため、新しい工場は建設予定地0,7,9に建てる必要があります。また、建設予定地0は大きな工場を立てます。
それぞれの顧客は、以下のように各工場に割り振ります。各工場から製品を顧客のもとへ配送します。
- 建設予定地0の工場: 顧客1, 5, 9, 10, 13, 14, 17, 19
- 建設予定地7の工場: 顧客0, 4, 6, 8, 11, 16
- 建設予定地9の工場: 顧客2, 3, 7, 12, 15, 18
このような「工場建設計画」と「顧客への配送計画」が、建設・製品配送に関わる総コストを最小化するための現状の最適解として提案されます。

例題に合わせて問題を解きましたが、現実はさらに制約が加わります。例えば、それぞれの顧客が発注する製品の数が月毎に異なる、各工場の生産キャパシティが異なる、などを考える必要も出てきます。
まとめ
この記事では、工場の建設計画を例に、整数計画法のひとつ「0-1整数計画法」を紹介しました。
- 整数計画問題は決定変数を整数として扱う数理計画問題
- 線形計画問題はP、整数計画問題はNP-hardに分類
- 線形計画法:実行可能領域(多面体)の端点に注目して最適解を決定
- 整数計画法:実行可能領域に含まれる整数の組み合わせのトライ&エラーから最適解を決定
今回の建設計画以外にも、整数計画法は、勤務表作成、生産計画、人員配置、施設配置計画、などにも広く利用されています。一方、どんな方法にも弱点があるように、線形・整数計画法にも課題はありますが、上手に扱えば、便利で強力な手法のひとつであることは間違いないと思います。
今後、他の利用例についてもまとめたいと考えています。

この記事は以上です。最後まで読んで頂きありがとうございました。
参考資料
(1): Winston, W. L., & Goldberg, J. B. (2004). Operations research: Applications and algorithms. Belmont, CA: Thomson/Brooks/Cole.
(2): 茨城 俊秀, 日本オペレーションズ・リサーチ学会, 特集 数理計画法 整数計画はなぜ難しい?, 1977
(3): 渡辺 治,ソフトウェアサイエンスの基本 シリーズ第3回 計算複雑さの研究って?, 2011
(4): CMI, P vs NP Problem (12/24/2021アクセス)


















この記事では、整数計画法を使ってある工場の建設計画問題を解いてみます。