オペレーションズ・リサーチの重要な分野である数理計画法は、数理計画問題(最適化問題)を解くための方法であり、データサイエンスにとっても大事なトピックです。
数理計画法は、制約条件を満たし、目的関数を最小、あるいは、最大にする最適解の発見を目的とし、通信、金融、製造、物流、輸送、ビジネスシステム、生物学的システム、天然資源マネジメント、など幅広い分野で利用されています。
- 数理計画問題と数理計画法の違いは何か
- 数理計画問題をどのように解くか
- PythonとGurobiをどうやって使うか
数理計画問題と数理計画法
数理計画問題(Mathematical programming problem)は
特定の集合上で定義された実数値関数または整数値関数についてその値が最小(もしくは最大)となる状態を解析する問題の総称
出典: Wikipedia, “最適化問題”
です。
数理計画問題は、現実問題を以下の関数と変数を使って数理モデルへと定式化し、最適解の取得を試みます。
- 目的関数 (Objective function)
- 決定変数 (Decision variables)
- 制約条件 (Constraints)
一方、数理計画法(Mathmatical programming: MP)は、数理計画問題を解く方法です。
数理計画法には、線形計画法(Linear programming: LP)、整数計画法(Intger programming: IP)、非線形計画法(Non-linear programming: NLP)、動的計画法(Dynamic programming: DP)などがあります。

数理計画問題=問題、数理計画法=手法、ということですね!
数理計画問題を解いてみよう
簡単な数理計画問題の例題を解いてみます。
数理計画問題を解くための流れは
- 現実問題の把握
- システム全体の観察
- 現実問題を数理モデルとして定式化
- アルゴリズムの開発
です。
例題
今回は、あるケーキ屋の売上予測の最大化を例にします。
あるケーキ屋は、自家製のミルクと卵を使って、チョコケーキとパウンドケーキの2種類を販売しています。
チョコケーキは400円、パウンドケーキは200円で販売します。
チョコケーキ1個を作るために、ミルク250ml、卵4個、オーブンで焼き時間20minが必要です。プレーンケーキ1個を作るためには、ミルク200ml、卵1個、焼き時間に50min必要です。
オーブンは1日に8h利用できます。
材料は、1日にニワトリから卵30個、ウシからミルク5L、を得られます。
ケーキ屋は、チョコケーキ、パウンドケーキをいくつ焼けば、売上予測を最大化できるでしょうか。
数理モデルの定式化
まず、この問題を数理モデルとして定式化します。
英語の大文字はクラス、小文字はインスタンスを表します。
Sets: 集合
\(C:\) Cakes ケーキ
\(I:\) Ingredients 材料
Data: データ
\(r_c:\) 各ケーキの販売価格 \(c \in C\)
\(a_i:\) 各材料の利用できる量 \(i \in I\)
\(u_{ic}:\) 各ケーキを作るために必要な材料の量 \(i \in I, \quad c\in C\)
Decision variables: 決定変数
\(x_c:\) 各ケーキを作る数 \(c \in C\)
Objective function: 目的関数→売上予測の最大化
\(maxmize: \quad 400x_{choc}+200x_{pound}\)
Constraints: 制約
オーブンの利用時間: \(20x_{choc}+50x_{pound} \leq 480\)
卵の数: \(4x_{choc}+1x_{pound} \leq 30\)
ミルクの量: \(0.25x_{choc}+0.2x_{pound}\leq 5\)
決定変数の範囲: \(x_{choc}\geq 0, \quad x_{pound}\geq 0\)
この数理モデルを可視化すると、Figure1のグラフが描けます。
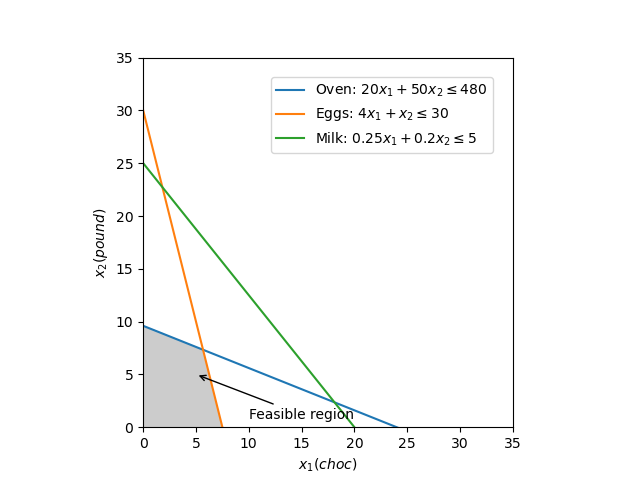
全ての制約を満たす範囲をグレーで色付けします。この範囲は実行可能領域(Feasible region)と呼ばれます。
最適解は、実行可能領域において、目的関数が最大となる決定変数になります。

ちなみに、\(c \in C\)は簡単な英語で「c in C」、「subset c of set C」と読んでいました。
アルゴリズムの実装
数理モデルが定式化できたら、それを解くためのアルゴリズムを実装します。

「数理最適化ソルバー:Gurobi Optimizer」を使えば、簡単なコードで数理計画問題を解けます。
- ケーキの個数は整数であり離散変数です。したがって、この問題を整数計画問題として解きます
- 24行目
m.addVar(vtype=GRB.INTEGER)は決定係数をint型として扱います
実装したアルゴリズムから\(x_1=6,\quad x_2=6, \quad max = 3600\)が得られます。
この結果から、例題の条件において、売上予測を最大化するためには、チョコケーキとパウンドケーキをそれぞれ6個作ることが最適で、そのときの売上は3600円であると分かります。


ただし、現実はこんな単純じゃないです。1)他の材料が必要、2)売上の変動、といった影響があるからです。数理計画法は、このような新しいデータ、視点の導入を繰り返しながら数理モデルを改良を改良し、取るべき行動を探索します。
まとめ
- 数理計画法はオペレーションズ・リサーチの一分野
- 数理計画問題=問題、数理計画法=手法
- 数理計画法のアプローチ
- 現実問題の把握
- 目的関数、決定変数、制約、を使って現実問題を数理モデルに定式化
- 数理モデルをアルゴリズムへ実装

数式に抵抗があるかもしれませんが、数理計画法は仕事にも役立つ大変便利な知識・スキルです。この記事を通じて、数理計画法に興味を持つ方が増えると嬉しいです。
この記事は以上です。最後まで読んでいただきありがとうございました。
参考資料
(1): Winston, W. L., & Goldberg, J. B. (2004). Operations research: Applications and algorithms. Belmont, CA: Thomson/Brooks/Cole.
(2): 京都大学 大学院情報学研究科 数理工学専攻 最適化数理分野 (7/19/2021アクセス)















この記事では、PythonとGroubi optimizerを使って数理計画問題を解きます。