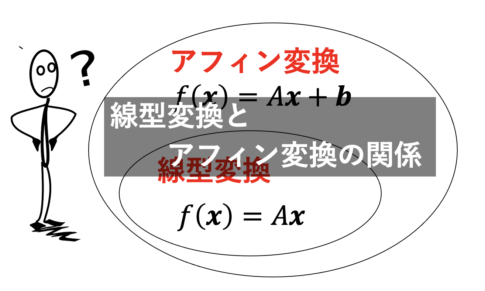
変換と行列:線形変換とアフィン変換の関係
線形代数における線形変換とは何か? 行列(マトリックス)を扱う線形代数は抽象度が高いうえ、3次元以上の可視化ができないため、海外の学生も理解に苦労していました。 この記事は、変換と行列の関係に注目して「線形変換とアフィン...
 統計・線形代数
統計・線形代数線形代数における線形変換とは何か? 行列(マトリックス)を扱う線形代数は抽象度が高いうえ、3次元以上の可視化ができないため、海外の学生も理解に苦労していました。 この記事は、変換と行列の関係に注目して「線形変換とアフィン...
 統計・線形代数
統計・線形代数高校・大学で学ぶテイラー展開は、機械学習でも利用されています。 テイラー展開は、無限級数を利用することで、任意の関数のある点近傍の値を近似します。この性質は、複雑な関数の周辺情報を獲得することに役立ちます。 この記事は「...
 統計・線形代数
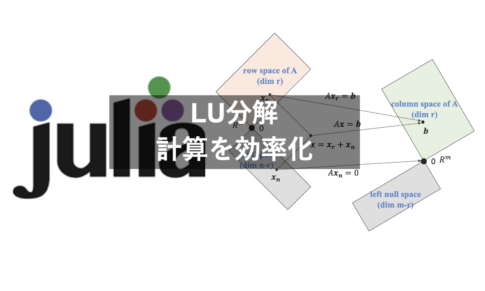
統計・線形代数LU分解は、正方行列を下三角行列と上三角行列の積に分解する方法です。 LU分解を利用すれば、連立一次方程式の計算をさらに効率化できます。 この記事は「LU分解」についてまとめます。 LU分解とは何か なぜLU分解が計算を...
 統計・線形代数
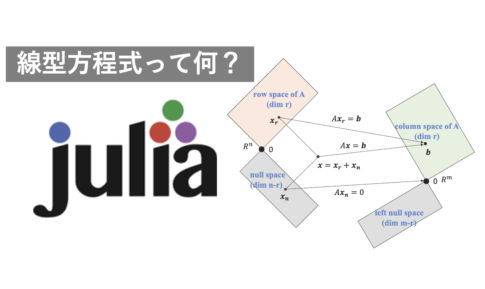
統計・線形代数ガウス・ジョルダン消去法、ガウス消去法は、連立一次方程式を解くための手法です。 学校の試験では、多くの人が連立一次方程式を自力で計算しています。 しかし、理工系の科学計算では、数百万以上におよぶ大規模な連立一次方程式を扱...
 統計・線形代数
統計・線形代数ビッグデータのような大規模データを扱うため、線形代数に関する知識・スキルが必要になります。 10年以上前に大学で線形代数を履修しましたが、その後、所属した化学系研究分野では、線形代数を利用する機会は皆無でした。 理系卒と...
 統計・線形代数
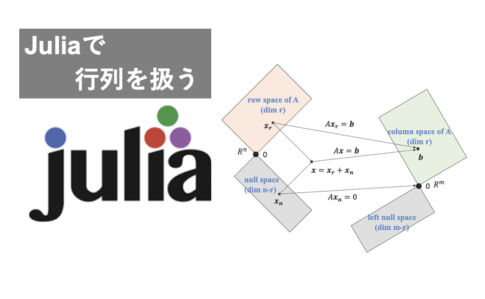
統計・線形代数行列は線形代数において最も重要なトピック。線形代数が”鬼”だとすると行列は”金棒”か。とにかく行列を理解しないことには線形代数は力を発揮できません。 この記事は「抑えておきたい行列の性質」と「Juliaを使った行列の扱い...
 統計・線形代数
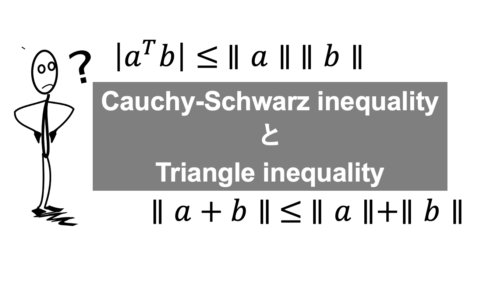
統計・線形代数コーシー・シュワルツの不等式はベクトルの内積とノルムの関係を、三角不等式は三角形の2辺の和の長さが残りの1辺の長さより必ず大きくなることを示します。 この記事は「コーシー・シュワルツの不等式」と「三角不等式」についてまと...
 統計・線形代数
統計・線形代数便利なライブラリ、パッケージのおかげで、データ解析は簡単に実行できる状況になっています。 しかし、semester2の「Mathmatics for Data Science」履修後に、「線形代数をもっと理解することで得...
 統計・線形代数
統計・線形代数ふと、線形代数と一緒にJuliaを学び直したいと思ったため、このシリーズでは、Juliaと線形代数をセットにしてまとめます。 Juliaに触れながら、なぜ線形代数がデータサイエンスにとって重要か少しでもお伝えできると嬉し...