ビッグデータのような大規模データを扱うため、線形代数に関する知識・スキルが必要になります。
10年以上前に大学で線形代数を履修しましたが、その後、所属した化学系研究分野では、線形代数を利用する機会は皆無でした。
理系卒といえど、分野によっては、線形代数が何のために、どのように利用されているか知らない人は多い気もします。
- 線形方程式・線形方程式系とは何か
- ベクトル・行列を使ってどうやって解を計算するか
- 計算過程の違いが計算時間にどのように影響するか
線形方程式
線形(線型)方程式(linear equation)は、全ての項の最大次数が1の式です。
線形方程式は$$ax+by = c$$と書けます。
\(x, y\)を変数(variable)、\(a, b, c\)を定数(constant)と呼びます。線形方程式は\(y=mx+n\)と表すことができ、eg.1より直線であることが分かります。
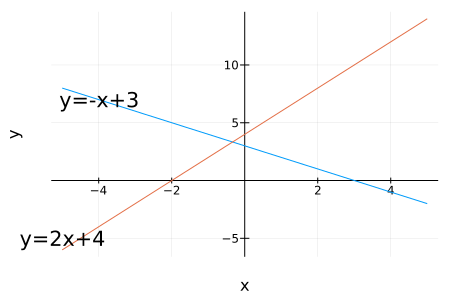
線形方程式系は複数の線形方程式(一次方程式)の組です。
\[\left\{
\begin{array}{rcrcrc@{\qquad}l}
x & + & y &= &3\\
2x & – & y &= &-4\\
\end{array}
\right.
\]
線形方程式系は行列表記できます。
$$
A \boldsymbol{x}=\boldsymbol{b}
$$
A=\begin{bmatrix}
1 & 1\\
2& -1
\end{bmatrix}, \quad
\boldsymbol{x} = \begin{bmatrix}
x\\
y\end{bmatrix}, \quad
\boldsymbol{b} = \begin{bmatrix}
3\\
-4\end{bmatrix}
\)です。 \(A\)を係数行列(coefficient matrix)、\(\boldsymbol{x}\)を解ベクトル(solution vector)、\(\boldsymbol{b}\)を定数項ベクトル(constant vector)と呼びます。

線形方程式系は「連立方程式系」や「連立一次方程式」とも呼ばれます。
解のパターン
線形方程式系には
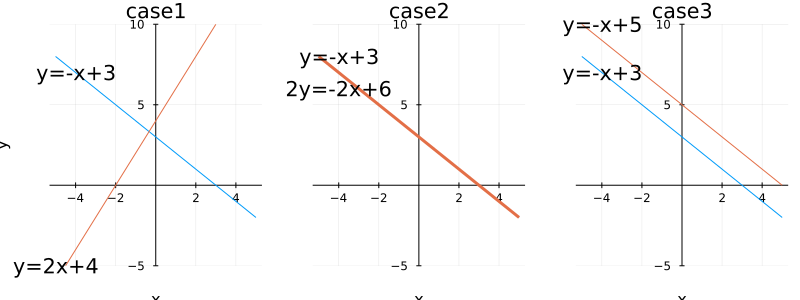
- 解が1組に決まる問題
- 解が無数にある問題
- 解が存在しない問題
の3パターンがあります。
問題を解くときは解のパターンを気にするようにします。
逆行列を使った計算
\(A\)が正則行列(regular matrix)の場合、逆行列(\(A^{-1}\))を持ちます。- \(A\)は正方行列
- \(det(A) \neq 0\)

逆行列(\(A^{-1}\))は、正方行列(\(A\))に対して左右どちらからかけても単位行列を作る行列です。
$$A^{-1}A=E \qquad AA^{-1}=E$$
$$\boldsymbol{x}=A^{-1}\boldsymbol{b}$$
Juliaでは、以下のコードから逆行列を使って\(\boldsymbol{x}\)を解けます。
det()は行列式(determinant)を計算します。- \(A\)が正則行列であれば、
inv()は逆行列を返します。inv(A)*xから\(\boldsymbol{x}\)を計算できます。 A \ bからも\(\boldsymbol{x}\)を計算できます。
inv()と\の計算時間を比較したところ、\の方がおよそ3倍速いようです。
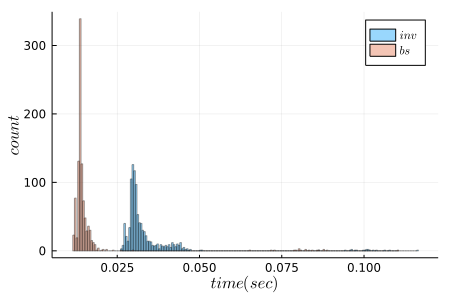
\はLU分解を適用しているため、inv()より計算が速いという話もありますが(4)、inv()について詳しく理解できていないです。
まとめ
- 線形方程式は最大次数が1次の式
- 線形方程式は直線
- 線形方程式系において、解のパターンは3つある
- 係数行列\(A\)が正則行列ならば、逆行列を使って解を計算できる
\はinv()より計算が速い
この記事は以上です。最後まで読んで頂きありがとうございました。
参考文献
(2) : Julia, “Linear Algebra” (6/27/2021アクセス)
(3) : 武内修@筑波大, “線形代数Ⅰ/連立一次方程式” (6/28/2021アクセス)
(4): stack overflow, “Inv() versus ‘\’ on JULIA” (6/29/2021アクセス)













この記事は「線形方程式(or 線形方程式)」についてまとめます。