行列は線形代数において最も重要なトピック。線形代数が”鬼”だとすると行列は”金棒”か。とにかく行列を理解しないことには線形代数は力を発揮できません。
- 行列とは何か
- Juliaで行列はどのように扱うか
目次
行列
定義
行列(Matrix)は、正方形や長方形の括弧の中に数や記号を含んだ2次元配列です。
$$\begin{bmatrix}
1 & 2 & 3 \\
7 & 0 & 0 \\
5 & 1 & 2
\end{bmatrix} \quad or \quad
\begin{pmatrix}
1 & 2 & 3 \\
7 & 0 & 0 \\
5 & 1 & 2
\end{pmatrix}$$
括弧の形に違いがありますが、意味は同じです。
行列の中のそれぞれの数字を要素(element)と呼びます。
\(A_{i,j}\)は行列\(A\)のi行、j列の要素の位置を指します。要素の位置を指定する\(i, j\)をインデックス(index)と呼びます。
例を示します。
\(A\)は\(2 \times 3 \)-行列です。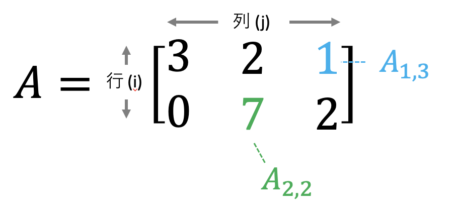
この場合、\(A_{1,3}\)は1行3列目の1、\(A_{2,2}\)は2行2列目の7を指します。
列ベクトルと行ベクトル
n-vectorは\(n \times 1\)-行列です。これを列ベクトル(column vector)と呼びます。
一方、\(1 \times n\)-行列は、行ベクトル(row vector)と呼びます。
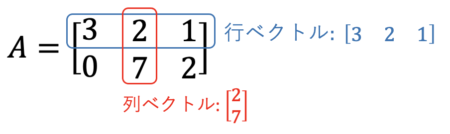
この場合、\(A\)の列ベクトルは2-column-vector、行ベクトルは3-row-vectorです。
行列の利用
実生活では様々なデータが行列としてまとめられています。
例えば、
- 顧客データ
- 生産記録
- 購入履歴
- 製薬の実験データ
- 画像
などです。
行列の種類
ある条件を満たした行列は以下の行列に分類されます。
- 零行列(Zero matrices)
全ての要素が0の行列 - 正方行列(square matrices)
行数と列数が等しい行列 - 単位行列(Identity matrices)
正方行列で対角に位置する要素が1、それ以外は0の行列 - 対角行列(Diagonal matrices)
正方行列で対角以外の要素が全て0の行列 - 三角行列(Triangular matrices)
正方行列で対角より下半分、あるいは、上半分が全て0の行列 - スパース行列(Sparse matrices)
大部分の要素が0の行列 - 転置行列(Transposed matrices)
\(m \times n\)-行列(\(A\))の行と列を入れ替えた行列。転置行列(\(A^T\))は\(n \times m\)-行列になる。

そういえばそんな用語があったなと段々思い出してきました。
行列の加算・減算
同じサイズ同士の行列は、加算・減算できます。
$$\begin{bmatrix}
1 & 2 \\
7 & 0 \\
5 & 1
\end{bmatrix} +
\begin{bmatrix}
3 & 4 \\
0 & 2 \\
1 & 1
\end{bmatrix}
= \begin{bmatrix}
4 & 6 \\
7 & 2 \\
6 & 2
\end{bmatrix}
$$
$$\begin{bmatrix}
8 & 3 \\
5 & 4
\end{bmatrix} –
\begin{bmatrix}
5 & 1 \\
2 & 0
\end{bmatrix}
= \begin{bmatrix}
3 & 2 \\
3 & 4
\end{bmatrix}
$$
覚えておきたい行列の性質として、
- \(A+B=B+A\)
- \((A+B)+C=A+(B+C)\)
- \(A+0=0+A=A\)
- \((A+B)^T=A^T+B^T\)
行列の乗算
スカラーと行列
スカラーは行列の全ての要素を乗算します。
$$3 \times
\begin{bmatrix}
1 & 2 \\
7 & 0 \\
5 & 1
\end{bmatrix} =
\begin{bmatrix}
3 & 6 \\
21 & 0 \\
15 & 3
\end{bmatrix}$$
覚えておきたい性質は、
- \((\beta + \gamma)A = \beta A+\gamma A\)
- \((\beta \gamma)A=\beta (\gamma A)\)
ベクトルと行列
\(A\)を\(m \times n\)-行列、\(x\)を\(n\)-vectorとすると、この行列とベクトルの積は\(y=Ax\)と表すことができます。出力される\(y\)は\(m\)-vectorです。 \(y\)の要素については、$$\begin{aligned}
y_{i}&=\sum_{k=1}^{n} A_{i k} x_{k}\\
&=A_{i 1} x_{1}+\cdots+A_{i n} x_{n}, \quad i=1, \ldots, m
\end{aligned}$$
です。例で示すと、
$$
\begin{aligned}
\begin{bmatrix}
y_1\\
y_2\\
y_3
\end{bmatrix}
&=
\begin{bmatrix}
1 & 2 \\
7 & 0 \\
5 & 1
\end{bmatrix}
\begin{bmatrix}
3 \\
1 \\
\end{bmatrix}\\
&= \begin{bmatrix}
(1)(3)+(2)(1)\\
(7)(3)+(0)(1)\\
(5)(3)+(1)(1)
\end{bmatrix}\\
&=\begin{bmatrix}
5\\
21\\
16
\end{bmatrix}
\end{aligned}
$$
となります。
\(m\times n\)-行列と\(p \times q\)-行列の積も同様です。積をとるために\(n=p\)である必要があります。行列同士の積から\(m \times q\)-行列が得られます。
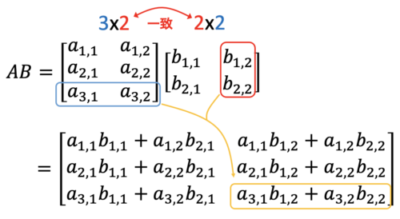
Juliaで行列を扱う
Juliaで行列を扱ってみます。
- 各括弧(
[])とセミコロン(;)を使って行列を作成します。 - 零行列は
zeros()を使って作ります。行数、列数を指定します。 - 単位行列は
Iを使って作成します。 - 対角行列は
Diagonal()で作成します。 - 三角行列は
UpperTrianglular()で上三角行列、LowerTriangular()で下三角行列を作成します。 - 転置行列は
Transpese()、またはシングルクォーテーション(')をつけることで作成します。 - 行列にピリオド(
.)をつけるとその行列の全ての要素を指定します。

線形変換と行列の関係について視覚的に理解するなら「3Blue1Brown」の動画がオススメなので参考にしてください。設定で日本語字幕をつけれます
まとめ
今回の記事で大事なポイントをまとめます。
- 行列は2次元配列
- 要素の位置はインデックスを使って指定
- 加算・減算するとき、それぞれの行列の行数と列数は同じであること
- \(m \times n\)-行列と\(p \times q\)-行列の積をとる場合、\(n = p \)であること
以上です。最後まで読んでいただきありがとうございました。
参考文献













この記事は「抑えておきたい行列の性質」と「Juliaを使った行列の扱い方」についてまとめます。