確率変数と確率分布：事象の発生確率を示す

統計用語を自分の言葉でもっと説明できるようになりたく、勉強のために本記事をまとめます。

この記事は「確率変数と確率分布」についてまとめます。

確率変数

確率変数

端的に、確率変数(Random variable)とは、ランダムに抽出したサンプルを扱う実験/調査から得る結果です。この結果は実数で、ランダムに得られます。

確率変数の定義を引用すると

確率変数とは、統計学の確率論において、起こりうることがらに割り当てている値(実数や整数)を取る変数。各事象は確率を持ち、その比重に応じて確率変数はランダムに値を取る。

Wikipedia, 確率変数

です。

確率変数をイメージしやすくするため、具体例をあげます。

あらゆる実験/調査を通じて、私たちは計測/観測から何らかの数値的な特徴を得ます。このような実験/調査の結果はある規則に関連して得られる、と考えることができ、これを確率で解釈できます。

例えば、大都市圏の電車で通勤するビジネスマン1000人から通勤時間を調査すると、それぞれの通勤時間に対してビジネスマンの確率が得られます。

また、100人の学生に１日にかかってくる電話の回数をアンケート調査すると、電話を受ける回数に対して学生の確率が得られます。

２つの例の調査から、ランダムに「通勤時間」や「電話を受ける回数」が実験/調査結果として得られます。この結果が確率変数です。

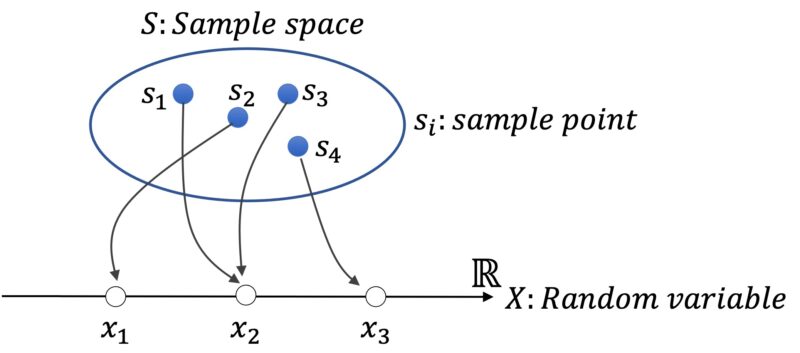
Figure1は確率変数の概念を示します。

\(S\)は標本全体の集合: 標本空間(Sample space)です。標本空間のそれぞれの点: 標本点(Sample point)\(s_i\)は、ランダムに確率変数\(x_i\)を得ます。

慣習的に、確率変数は\(X\)や\(Y\)の大文字で記述します。一方、計測/観測から得られた数値は\(x\)や\(y\)の小文字で記述します。変数\(x\)は確率変数\(X\)の値です。

Figure1の例だと、\(X=x_1\)となる標本点は、標本空間に含まれる４つの標本点のうち\(s_2\)だけです。したがって、\(\mathbb{P}(X=x_1)=\frac{1}{4}\)と確率で表せます。

離散型確率変数と連続型確率変数

確率変数には２種類あります。一つが確率変数が離散量の離散型確率変数 (Discrete random variable)、もう一つが確率変数が連続量の連続型確率変数 (Continuous random variable)です。

例えば、整数だけで得られる数や回数などのデータは、離散型確率変数として扱います。小数点を含む大きさ、重さ、温度などのデータは、連続型確率変数として扱います。

確率分布

確率変数\(X\)を横軸に、確率変数から得られる確率を縦軸にヒストグラムを描くと、確率の分布情報が得られます。これを確率分布(Probability distribution)と呼びます。

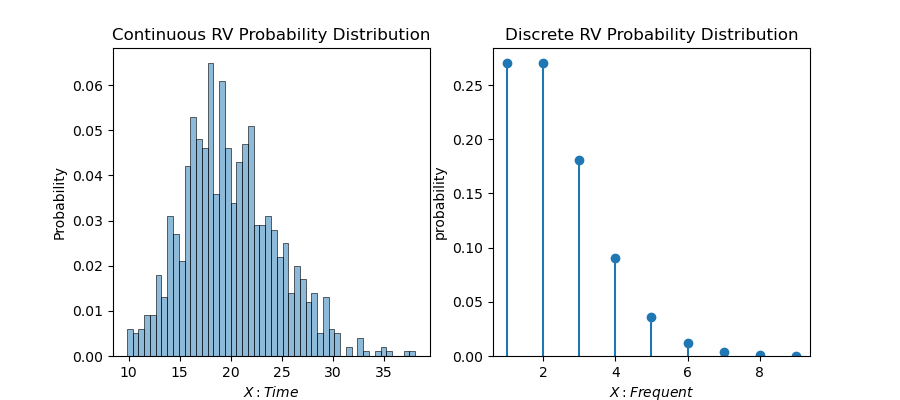
確率分布は、統計学、物理学など、様々な分野で利用されています。

確率分布はどのような時に利用しますか？

確率分布を利用するケースとして、主に以下３つが考えられます。

1. 確率の予測：確率分布はある事象が発生する確率を数値化するため、確率の予測に利用できます。この性質を利用することで、事象の発生確率を予測できます。
2. データの特徴把握：データの確率分布を確認することで、そのデータの特徴を把握できます。例えば、正規分布に従うデータであれば、平均値と標準偏差からデータの中心とばらつきを把握できます。
3. モデルの検証：統計モデルは、データがどのような分布に従うか仮定します。統計モデルを作成する前に、仮定が適切であるか検証できます。

まとめ

この記事は、確率変数と確率分布についてまとめました

最近はChatGPTの進化が目覚ましく、勉強方法に悩みますが、時間かけながら理解した内容は無駄にならないと信じてコツコツ復習します。

この記事は以上です。最後まで読んで頂きありがとうございました。

参考資料

(1)Jay L. Devore, Kenneth N. Berk, Modern Mathematical Statistics with Applications, 2011