線形代数で扱う射影は、高次元のデータセットに対する様々な数学演算の理解に役立ちます。
機械学習、数値計算において、射影の代表的な利用例には線形回帰、特異値分解などがあげられ、その利用は幅広いです。
射影

射影って何でしょう?
射影: Projectionとは、ベクトルに光を当てて\(n\)次元の部分空間に影を作ること、または影です。
例として、2つのベクトル\(\boldsymbol{a},\boldsymbol{b}\)をおき、\(\boldsymbol{a}\)上への\(\boldsymbol{b}\)の射影を考えます。
このとき、\(\boldsymbol{p}\)が\(\boldsymbol{a}\)上にできる\(\boldsymbol{b}\)の射影です。
\(\boldsymbol{e}\)は射影誤差: Projection errorです。射影誤差は、\(\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}\)の関係にあります。射影誤差は\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の最短距離になります。

\(\boldsymbol{p}\)は\(\boldsymbol{a}\)上に存在することから、\(\boldsymbol{p}\)の値が分からなくても
$$\boldsymbol{p} =\boldsymbol{a}\cdot \frac{\boldsymbol{a}^T\boldsymbol{b}}{\boldsymbol{a}^T \boldsymbol{a}}$$
から\(\boldsymbol{p}\)を求めることができます。
部分空間への射影
\(A\)を\(3\times2\)の行列、\(\boldsymbol{x}\)を2次元のベクトル、\(\boldsymbol{b}\),\(\boldsymbol{p}\)を3次元のベクトルとおきます。
そして\(\boldsymbol{b}\)はカラムスペース\(C(A)\)に存在せず、\(A\boldsymbol{x}=\boldsymbol{b}\)が解けないケースを考えます。
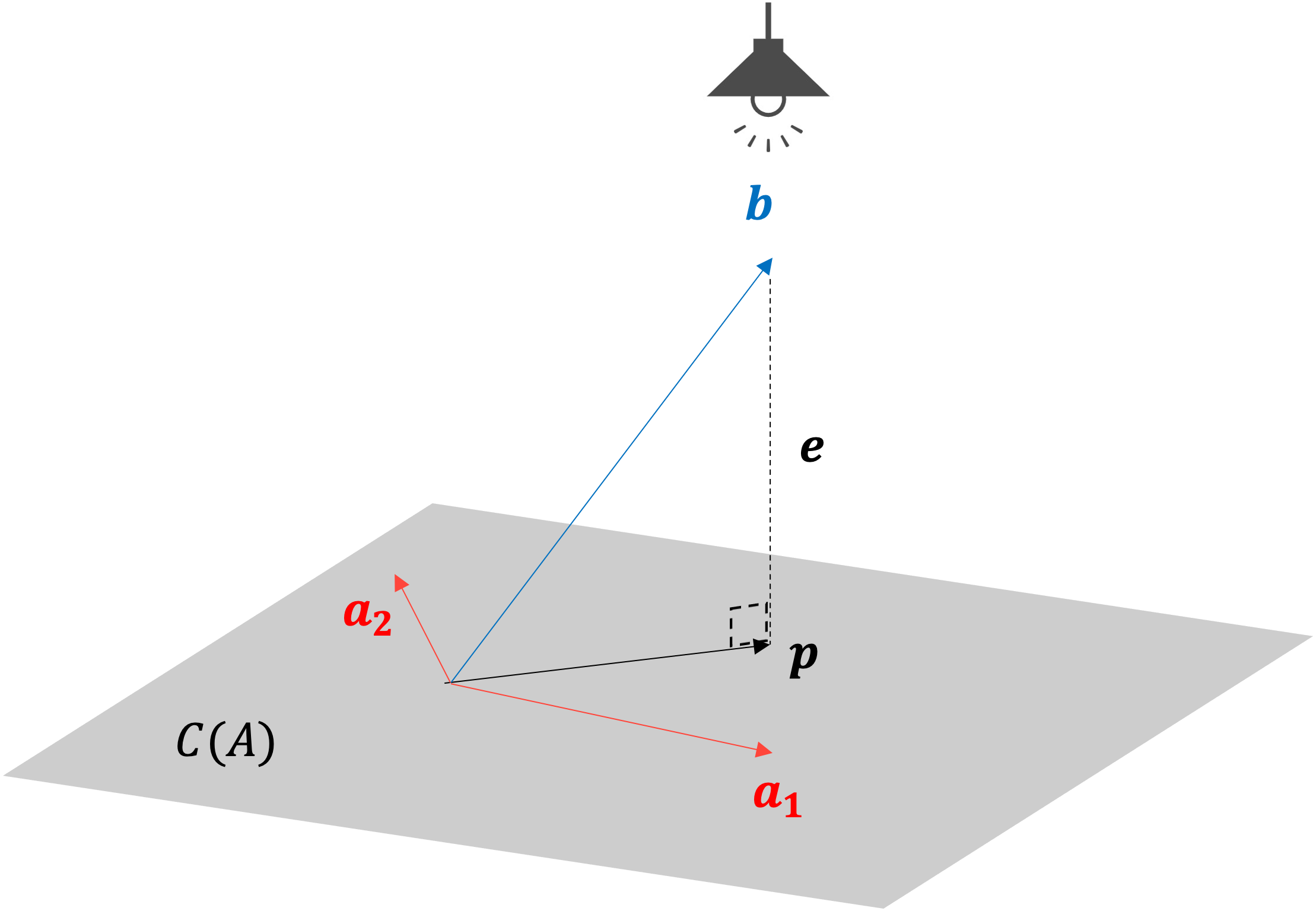
\(A\boldsymbol{x}=\boldsymbol{b}\)を満たす\(\boldsymbol{x}\)が存在しない状況において、射影は射影誤差が最小となる\(\hat{\boldsymbol{{x}}}\)を導きます。

どうやって\(\hat{\boldsymbol{{x}}}\)を見つけるんでしょう?
以下3つの条件を整理します。
- \(\boldsymbol{p}\)は\(C(A)\)上に存在: \(\boldsymbol{p}=A\hat{\boldsymbol{x}}\)
- \(\boldsymbol{e}\)と\(C(A)\)は垂直: \(A^T\boldsymbol{e}\)=0
- \(\boldsymbol{e}\)は\(\boldsymbol{b}\)と\(\boldsymbol{p}\)で表現可能: \(\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}\)
まず
$$\begin{eqnarray}\boldsymbol{e}&=&\boldsymbol{b}-\boldsymbol{p}\\
&=& \boldsymbol{b}-A\hat{\boldsymbol{x}}\end{eqnarray}$$
と変換できます。
続いて
$$\begin{eqnarray}A^T\boldsymbol{e}&=& A^T(\boldsymbol{b}-A\hat{\boldsymbol{x}})\\
&=& 0 \end{eqnarray}$$
となります。このことから
$$A^TA \hat{\boldsymbol{x}}=A^T \boldsymbol{b}$$
です。
もし\(A\)が線形独立であれば、\(A^TA\)は逆行列を持ち、
$$\hat{\boldsymbol{x}}=(A^TA)^{-1}A^T \boldsymbol{b}$$
が得られます。

\(\hat{\boldsymbol{x}}\)が分かると、射影誤差が最短となる\(\boldsymbol{p}\)が得られます。
\(\boldsymbol{p}=A\hat{\boldsymbol{x}}\)より
$$\boldsymbol{p}=A(A^TA)^{-1}A^T \boldsymbol{b}$$
から射影誤差\(\boldsymbol{e}\)が最短となる\(\boldsymbol{p}\)が得られます。
\((A^TA)^{-1}A^T=A^\dagger\): 擬似逆行列: pseudo-inverse matrixとおけます。
さらに
$$\begin{eqnarray}A(A^TA)^{-1}A^T&=& A A^\dagger \\
& = & P\end{eqnarray}$$
\(P\):射影行列: Projection matrixに変換できます。
射影行列\(P\)を使って
$$\boldsymbol{p}=P\boldsymbol{b}$$
と表すことができます。

射影の性質は分かりましたが、具体的にどういうことに利用できるんでしょう?

機械学習において、射影は線形回帰や特異値分解などの計算に利用されています。一例として最小二乗法をまとめます。
最小二乗法
最小二乗法: Least square methodは、実測値\(y_i\)と予測値\(\hat{y_i}\)の残差の和が最小となる線形回帰のパラメータ: \(\beta_0,\beta_1\)を推定する方法です。
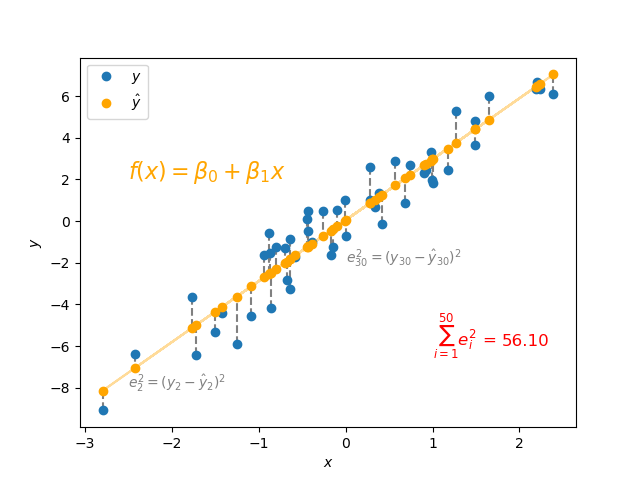
取得したい線形回帰を\(f(x)=\beta_0 + \beta_1 x\)とおきます。
$$X = \begin{bmatrix}1 & x_1\\
1&x_2\\
\vdots & \vdots \\
1&x_m
\end{bmatrix} \quad \boldsymbol{\beta}= \begin{bmatrix}\beta_0\\\beta_1\end{bmatrix}\quad
\boldsymbol{y}= \begin{bmatrix}y_0\\ y_1\\ \vdots\\ y_m\end{bmatrix}$$
とおくと、この回帰直線を線形代数では
$$X \boldsymbol{\beta} = \boldsymbol{y}$$
と表せます。

\(X\)を計画行列: Design matrixとも呼びます。
繰り返しになりますが、取得したい線形回帰のパラメータ: \(\hat{\boldsymbol{\beta}}\)は、実測値: \(\boldsymbol{y}\)と線形回帰から得られる予測値: \(\hat{\boldsymbol{y}}\)の残差の和が最小となります。
つまり
$$||\boldsymbol{e}||^2=min(e_1^2+\cdots+e_m^2)$$
を満たします。
ここで残差の和を最小とする\(\hat{\boldsymbol{\beta}}\)を導くために射影を利用します。
線形回帰のパラメータ: \(\hat{\boldsymbol{\beta}}\)は射影を使って
$$\hat{\boldsymbol{\beta}}=(X^TX)^{-1}X^T \boldsymbol{y}$$
から計算できます。
また、\(\hat{\boldsymbol{y}}=P\boldsymbol{y}\)から
射影行列を利用することで回帰直線上の\(\hat{\boldsymbol{y}}\)の値を計算できます。

以下は射影と最小二乗法の動作確認のためのpythonのコードです。
以下の過程からも同様の関係式を導けます。
残差平方和は
$$||\boldsymbol{e}||^2=||X\hat{\boldsymbol{\beta}} – \boldsymbol{y}||^2$$
です。
これを展開すると
$$\begin{eqnarray}e^Te &=& (X\hat{\boldsymbol{\beta} }- \boldsymbol{y})^T(X\hat{\boldsymbol{\beta}} – \boldsymbol{y}) \\
&=& \hat{\boldsymbol{\beta}}^TX^T X\hat{\boldsymbol{\beta}}-\hat{\boldsymbol{\beta}}^TX^T\boldsymbol{y}-\boldsymbol{y}^TX\hat{\boldsymbol{\beta}}+\boldsymbol{y}^T\boldsymbol{y}\\
&=& \hat{\boldsymbol{\beta}}^TX^T X\hat{\boldsymbol{\beta}}-2\hat{\boldsymbol{\beta}}^TX^T\boldsymbol{y}+\boldsymbol{y}^T\boldsymbol{y}\\
\end{eqnarray}$$
です。
最小値を取るため、微分した展開式は0です。
$$\begin{eqnarray}\frac{d e^Te}{d\hat{\boldsymbol{\beta}}}&=&2X^TX\hat{\boldsymbol{\beta}}-2X^T\boldsymbol{y}\\
& =& 0
\end{eqnarray}$$
つまり
$$X^TX\hat{\boldsymbol{\beta}}=X^T\boldsymbol{y}$$
であり、\(X\)がフルランクの行列であれば
であり、\(X\)がフルランクの行列であれば逆行列を持ち
$$\hat{\boldsymbol{\beta}}=(X^TX)^{-1}X^T\boldsymbol{y}$$
が得られます。

データセットが大きくなると計算効率が課題に上がります。アルゴリズムの計算効率化のためにQR分解やコレスキー分解を利用する方法があります。
まとめ
この記事は射影と最小二乗法についてまとめました。
- 射影
- ベクトルに光を当てて\(n\)次元の部分空間に影を作る
- \(A(A^TA)^{-1}A^T \boldsymbol{b}\)から射影誤差を最短とする\(\boldsymbol{p}\)を得る
- 最小二乗法
- 実測値と予測値の残差の和が最小となる線形回帰のパラメータを推定する方法
- 線形回帰において\((X^TX)^{-1}X^T\boldsymbol{y}\)から\(\hat{\boldsymbol{\beta}}\)を得る
線形代数と機械学習の勉強前だと、何となくエクセルで回帰直線のパラメータを扱っていましたが、素人ながら導出方法が分かると線形代数の面白さを感じた次第です。
この記事は以上です。最後まで読んでいただきありがとうございました。
参考資料
(1) D.P. Kroese, Z.I. Botev, T. Taimre, R. Vaisman. Data Science and Machine Learning: Mathematical and Statistical Methods, Chapman and Hall/CRC, Boca Raton, 2019.






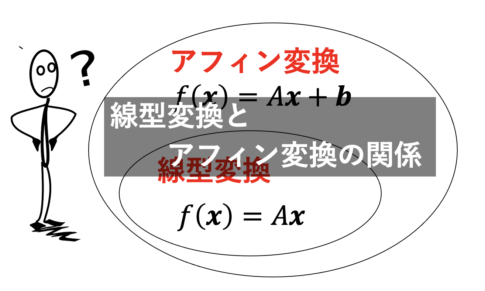







射影がどのように利用されているのか。この記事は「射影の性質と最小二乗法」についてまとめます。