一般化線形モデル(Generalized Linear Model: GLM)のコンセプトの学習は、確率分布を統計モデルにどのように組み込むか考え始める機会に繋がります。
では、一般線形回帰モデル(General Linear Model)とGLMが違うポイントは何でしょう。
- 一般線形モデルと一般化線形モデル(GLM)の違いは何か
- どんなケースでGLMを扱うか
目次
一般線形モデルと一般化線形モデルの違い
一般化線形モデル(Generalized Linear Model: GLM)は、線形回帰モデルをより柔軟に一般化した統計モデルです。線形回帰モデルは、「線形回帰」「一般線形モデル」とも呼ばれます。
線形回帰モデルは、ランダムに生じる誤差の分布(誤差構造)を\(\mathbb{E}[\boldsymbol{\varepsilon}]=0, Var(\boldsymbol{\varepsilon})= \sigma^2\)の正規分布に従う確率変数として扱うモデルです。
一方、一般化線形モデル: GLMは、正規分布を含む、ポアソン分布 (Poisson distribution)、ガンマ分布 (Gamma distribution)、二項分布 (Binomial distribution)などの指数型分布族 (Exponential distribution family)から誤差構造を選択できます。

GLMは線形回帰モデルを拡張した統計モデルと捉えることができます。線形回帰、線形回帰モデル、一般線形モデルが説明されるとき、多くの場合、誤差構造は正規分布と仮定しています。
線形回帰モデルの特徴
まず基本となる線形回帰モデルの特徴をまとめます。
概要
線形回帰モデル(Linear regression model)は以下3つの要素から構成されます。
- 応答変数 (Resoponse variable): 従属変数、出力変数とも呼ぶ。\(Y\)を観測値\(y\)の確率変数として表記する。 \(Y\)は正規分布に従うと仮定する。\(y \sim \mathcal{N}(\mu,\sigma^2)\)
- 説明変数(Explanatory variable): 独立変数、入力変数とも呼ぶ。\(p\)個の次元を持つベクトル。\(\mathbf{x}=[x_1,x_2,\cdots,x_p]\)とおく。
- パラメーター(Parameter): \(p+1\)個の次元を持つベクトル。\(\boldsymbol{\beta} = [\beta_0,\beta_1, \cdots, \beta_p]^T\)とおく。
応答変数\(y\)は、説明変数\(x\)に従属し、
$$\begin{equation}y_i=\beta_0 + \beta_1x_{i,1}+\cdots+\beta_p x_{i,p}+\varepsilon_i \tag{1}\end{equation}$$
と表せます。
説明変数が1つの線形回帰モデルを「単回帰モデル(Simple linear regression)」、説明変数が2つ以上の線形回帰モデルを「重回帰モデル(Multiple linear regression model)」と呼びます。
誤差項\(\varepsilon\)は、\(\varepsilon \sim \mathcal{N}(0,\sigma^2)\)の正規分布と仮定します。
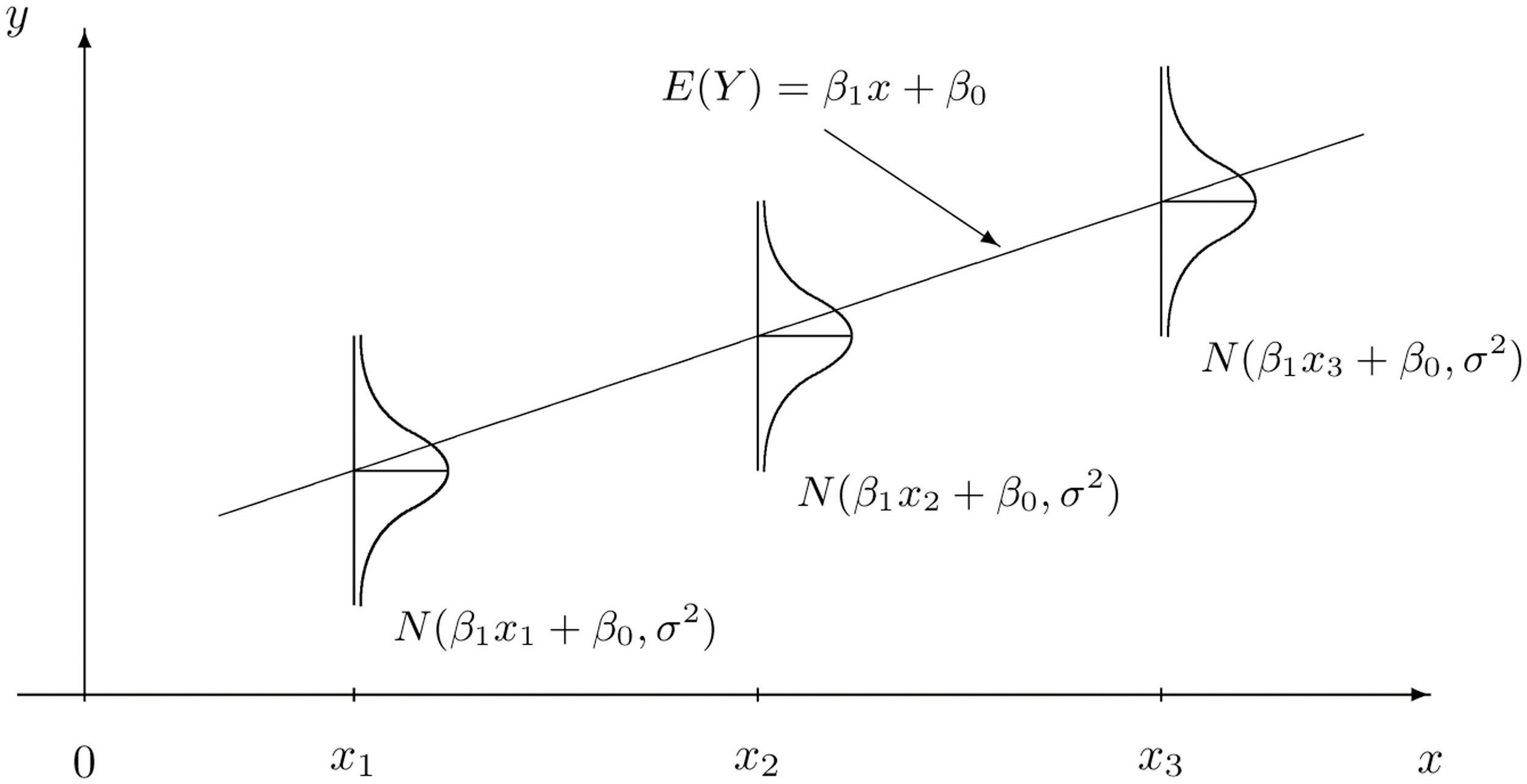
説明変数\(x\)の任意の値を\(x^{*}\)とおくと、このときの\(Y\)の期待値\(\mu_{Y\cdot x^{*}}\)と分散\(\sigma^2_{Y\cdot x^{*}}\)は
\(\begin{eqnarray}\mu_{Y\cdot x^{*}}&=& \mathbb{E}[Y|x=x^{*}]\\
&=& \mathbb{E}[\beta_0 + \beta_1x^{*}_1+\cdots+\beta_p x^{*}_p+\varepsilon]\\
&=& \beta_0 + \beta_1x^{*}_1+\cdots+\beta_p x^{*}_p + \mathbb{E}[\varepsilon]\\
&=& \beta_0 + \beta_1x^{*}_1+\cdots+\beta_p x^{*}_p \end{eqnarray}\)
\(\begin{eqnarray}\sigma^2_{Y\cdot x^{*}}&=& Var(Y|x=x^{*})\\
&=& Var(\beta_0 + \beta_1x^{*}_1+\cdots+\beta_p x^{*}_p+\varepsilon)\\
&=& Var(\beta_0 + \beta_1x^{*}_1+\cdots+\beta_p x^{*}_p) + Var(\varepsilon)\\
&=& 0+\sigma^2 \\
&=& \sigma^2 \end{eqnarray}
\)
です。
つまり、応答変数\(Y\)の期待値\(\mu\)は、\(x\)についての線形モデル関数であることが分かります。
また、
$$
\mathbf{Y} = \begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix},\quad
\mathbf{X} = \begin{pmatrix}1 & \mathbf{x}_1\\1 & \mathbf{x}_2\\\vdots&\vdots\\1 & \mathbf{x}_n\end{pmatrix}, \quad
\boldsymbol{\beta} = \begin{pmatrix}\beta_0\\\beta_1\\\vdots\\\beta_p\end{pmatrix},\quad
\boldsymbol{\varepsilon} = \begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\vdots\\\varepsilon_n\end{pmatrix}
$$
とおくと、\((1)\)は
$$\begin{equation}\mathbf{Y}=\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon}\tag{2}\end{equation}$$
の行列表記で表せます。
線形回帰モデルの最適化パラメータ\(\hat{\boldsymbol{\beta}}\)は、観測値と推測値の残差を最小にする値です。多くのケースで最小二乗法を用いて計算します。
$$||\boldsymbol{\varepsilon}||^2 = ||\mathbf{Y}-\mathbf{X}\hat{\boldsymbol{\beta}}||^2$$

\(Y=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\varepsilon\)も線形回帰モデルに分類されます。応答変数\(Y\)を説明変数\(X\)と\(\beta\)の線形結合から得るためです。
モデルの用途

どんな目的で線形回帰モデルを利用するんでしょうか?
線形回帰モデルを利用する目的は大きく2点あります。
- 説明変数を利用した応答変数の予測
- 説明変数が応答変数の変動に寄与する大きさの説明
線形モデルは単に応答変数を予測するだけでなく、説明変数と応答変数の関係を考察するための統計手法として利用します。
線形回帰モデルの強みと弱み
線形回帰モデルの強みと弱みをまとめます。
現実のデータの分布は歪むこともあり、誤差構造が常に正規分布とは限りません。この課題を解決するため、一般化線形モデル: GLMを扱います。

データセットのインスタンスの数を\(n\)、扱う説明変数の数を\(m\)とすると、線形回帰モデルのトレーニングと予測の時間計算量は\(O(nm^2 + m^3)\)、\(O(m)\)です。
一般化線形モデル: GLMの特徴
本題の一般化線形モデル: GLMの特徴をまとめます。
概要
GLMは3つの要素から構成され、線形回帰モデルと少々扱いが異なります。
- 確率分布(Probability distribution): 各々の値を取る確率を示す分布。GLMでは、誤差構造が指数型分布族(Exponential distribution family)と仮定する。
- 線形予測子(Linear predictor): 説明変数\(\mathbf{X}\)とパラメーター\(\boldsymbol{\beta}\)の線形結合。\(\eta = \mathbf{X}\boldsymbol{\beta}\)。
- リンク関数(Link function): \(\mathbb{E}[\mathbf{Y}|\mathbf{X}]= \mu\)と線形予測子\(\eta\)が対応するように変換する関数\(g(\cdot)\)。\(g(\mu)=\eta\)を満たす。
リンク関数は、指数型分布族の確率分布を持つ応答変数\(\mathbf{Y}\)の期待値(平均)\(\mu\)を説明変数\(\mathbf{X}\)とパラメーター\(\boldsymbol{\beta}\)の線形結合\(\mathbf{X}\boldsymbol{\beta}\)で説明可能にします。
数式としてまとめると
$$\mu =g^{-1}(\mathbf{X}\boldsymbol{\beta})$$
の関係を成立します。
パラメーターを推定するために最小二乗法を利用しましたが、ロジスティック回帰モデル、ポアソン回帰モデルでは、パラメーターの推定に最尤法(Maximum likelihood)を利用します。

GLMでは、誤差構造の確率分布を仮定し、リンク関数を決定します。
リンク関数の種類

リンク関数にはどのような種類があるんでしょう?
ここでは、GLMで扱う代表的な指数型分布族の確率分布とリンク関数をまとめます。
GLMで扱う指数型分布族に
- 正規分布: Normal distribution
- 指数分布: Exponential distribution
- ガンマ分布: Gamma distribution
- ポアソン分布: Poisson distribution
- ベルヌーイ分布: Bernouli distribution
- 二項分布: Binomial distribution
- カテゴリカル分布: Categorical distribution
が代表的な例として挙げられます。(9)
| 確率分布 | 分布範囲 | 利用例 | リンク関数 \(g(\mu)=\mathbf{X}\boldsymbol{\beta}\) | \(\mathbb{E}[\mathbf{Y}|\mathbf{X}]:\) \(\mu=g^{-1}(\mathbf{X}\boldsymbol{\beta})\) |
|---|---|---|---|---|
| 正規分布 | \(\mathbb{R}:(-\infty, +\infty)\) | 線形応答のデータ | \(\mu=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=\mathbf{X}\boldsymbol{\beta}\) |
| 指数分布 | \(\mathbb{R}:(0, +\infty)\) | 指数応答のデータ | \(-\mu^{-1}=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=-(\mathbf{X}\boldsymbol{\beta})^{-1}\) |
| ガンマ分布 | \(\mathbb{R}:(0, +\infty)\) | 指数応答のデータ | \(-\mu^{-1}=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=-(\mathbf{X}\boldsymbol{\beta})^{-1}\) |
| 逆ガウス分布 | \(\mathbb{R}:(0, +\infty)\) | 鋭いピークやテーリングするデータ ファイナンス、保険、地質学etc.. | \(\mu^{-2}=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=(\mathbf{X}\boldsymbol{\beta})^{-1/2}\) |
| ポアソン分布 | \(\mathbb{Z}:0,1,2,\cdots\) | 定めた時間中の発生回数 | \(ln(\mu)=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=exp(\mathbf{X}\boldsymbol{\beta})\) |
| ベルヌーイ分布 | \(\mathbb{Z}:{0,1}\) | yes, noの2択の解答 | \(ln(\dfrac{\mu}{1-\mu})=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=\dfrac{1}{1+exp(-\mathbf{X}\boldsymbol{\beta})}\) |
| 二項分布 | \(\mathbb{Z}:0,1,\cdots,N\) | N個の質問中のyesの出現数 | \(ln(\dfrac{\mu}{n-\mu})=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=\dfrac{1}{1+exp(-\mathbf{X}\boldsymbol{\beta})}\) |
| カテゴリカル分布 | \(\mathbb{Z}:[0,K)\) \(\mathbb{Z}:[0,1]\)の\(K\)ベクトル | K個ある解答パターンの頻度 | \(ln(\dfrac{\mu}{1-\mu})=\mathbf{X}\boldsymbol{\beta}\) | \(\mu=\dfrac{1}{1+exp(-\mathbf{X}\boldsymbol{\beta})}\) |
応答変数\(\mathbf{Y}\)の確率分布を正規分布と仮定すれば、GLMで線形回帰モデルを扱っていることになります。
GLMを利用するケース

GLMはどういったケースで利用するんでしょう?
GLMは線形回帰モデルの仮定(誤差構造が正規分布という仮定)に従わないときに利用します。
より具体的には、
(1)\(\mathbf{X}\)と\(\mathbf{Y}\)のグラフが非線形
(2)誤差構造が非正規分布
(3)\(\mathbf{Y}\)が離散型データ・カテゴリカルデータ
の3つのいづれかのケースで起こります。
例えば、応答変数\(\mathbf{Y}\)がカウントデータを扱う場合、0以上の離散型変数で、確率分布も離散型である必要があります。このとき、誤差構造がポアソン分布に従うと仮定すると、リンク関数はlog関数となります。
リンク関数は\(g(\mu)=ln(\mu)=\mathbf{X}\boldsymbol{\beta}\)です。
したがって、\(\mu\)は
$$\mu = exp(\mathbf{X}\boldsymbol{\beta})$$
となります。
Pythonで実装するGLM
「新作のパンを店頭に出した日からの経過日数と新作のパンが売れた個数」を例に、PythonでGLMを扱ってみます。
Figure1の左図は応答変数\(\mathbf{Y}\)の確率分布を、右図は店頭に新作のパンを置いた経過日数\(\mathbf{X}\)と新作のパンが売れた個数\(\mathbf{Y}\)を示す散布図です。
(1)\(\mathbf{X}\)と\(\mathbf{Y}\)の関係が非線形、(2)データの分布が正規分布ではない、(3)\(\mathbf{Y}\)が離散型データ、ですから、このデータは線形回帰モデルの仮定に当てはまらないと分かります。
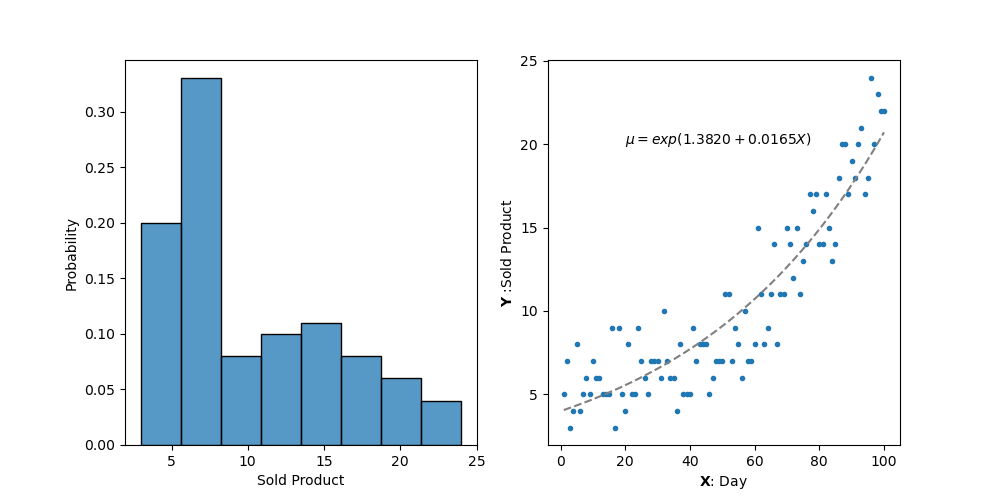
以下、Pythonで統計モデルを扱う際に利用するstatsmodelを使用して右図のパラメーターを得ます。(11)
sm.families.links.<link_nama>はリンク関数を決定します。sm.families.<family_name>から確率分布を決定します。
sm.add_constant()は切片\(\beta_0\)を加えるために、計画行列\(\mathbf{X}\)に指示変数が全て1のカラムを追加します。
statsmodelではGLMの推計結果をres.summary()から以下の形式で得られます。
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: Sold Product No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0000
Method: IRLS Log-Likelihood: -225.77
Date: Wed, 17 Aug 2022 Deviance: 46.279
Time: 14:18:37 Pearson chi2: 47.0
No. Iterations: 4
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.3820 0.080 17.282 0.000 1.225 1.539
Day 0.0165 0.001 14.259 0.000 0.014 0.019
==============================================================================
ここで得た結果をどう解釈すればいいのでしょう?
以下、それぞれの項目の意味をまとめます。
- Dep. Variable: 従属変数(応答変数)
- Model: モデル名
- Model Family: 設定した確率分布
- Link Function: 設定したリンク関数
- Method: 最適化パラメーターを得るために使用した方法。IRLS: Iteratively reweighted least squares estimation.
- Date: モデルを作成した日
- Time: モデルを作成した時間
- No. Interactions: Methodで反復した回数
- Covariance Type: 共分散のタイプ。デフォルトでは
cov_type='nonrobust' - No. Observation: サンプルの大きさ
- Df Residuals: 残差の自由度。(サンプル数)-(推定パラメーター数): \(n-p-1\)
- Df Model: Degree of Freedom。モデルの自由度。モデルに使用する説明変数の数。
- Scale: Disperation。分布の広さ、狭さを示す。Likelihood modelの場合、常に1になる。疑似尤度推定のときに変化するそう。
- Log-Likelihood: 対数尤度。モデルのフィッティングの良し悪しを示す。値が大きいほどデータに対してフィッテイングが良いと判断。
- Deviance: 統計モデルの良し悪しを判断。値が小さいほど、モデルの当てはまりが良いと判断。Devianceを\(D\)、尤度を\(L\)、提案モデルを\(M\)、フルモデルを\(S\)と記述すると\(D_{M}=-2(logL_{M}-logL_{S})\)。
- Person chi2: モデルの良し悪しを判断。尤度比検定(Likelihood ratio test)。帰無仮説のモデルと対立仮説のモデルの対数尤度の差がカイ2乗分布に漸近的に従うことを利用。説明変数の有無の影響(推定するパラメーターの差の影響)を見ている。
まとめ
この記事は、一般化線形モデル:GLMについてまとめました。
- GLMは誤差構造を指数型分布族から選択するモデル
- 一般線形回帰は誤差構造を正規分布と仮定するモデル
- GLMは、確率分布、線形予測子、リンク関数の3つから構成
- GLMの確率分布の平均は線形予測子とリンク関数に依存

気軽に扱っている回帰モデルも、深く掘り下げていくと奥が深いことが分かりました。まだまだ理解不足ですので、誤った点があればご指摘いただけると幸いです。
この記事は以上です。最後まで読んでいただきありがとうございました。
参考資料
(1) Trevor Hastie, Robert Tibshirani, Jerome Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2009
(2) Dirk P. Kroese, Zdravko Botev, Thomas Taimre, Radislav Vaisman, Data Science and Machine Learning: Mathematical and Statistical Methods, 2020
(3) Jay L. Devore, Kenneth N. Berk, Modern Mathematical Statistics with Applications, 2011
(5)久保拓弥, データ解析のための統計モデリング, 久保講義のーと 2008–11–06
(6)大東健太郎, 線形モデルから一般化線形モデルへ, 雑草研究 Vol55(4) 268-274, 2010
(7)Ron Sarafian, Introduction to Data Science, December 2, 2020
(9)Wikipedia, Generalized linear model
(10)Wikipedia, Iteratively reweighted least squares









この記事は「一般化線形モデルの特徴」についてまとめます。