統計: 記述統計と推測統計の違いは何か？

統計はデータの中から注目すべきポイントやパターンの発見を手助けします。

一方、たびたび耳にする「記述統計」と「推測統計」というワード。統計の基礎と言われますが、他人に違いを説明しようとすると、分かっているようで分かっていないと思ったので、要点を記事にまとめたいと思います。

この記事は「記述統計と推測統計」についてまとめます。

そもそも統計とは？

データから新たなインサイトを獲得するため、あるいは重要な意思決定を行うために統計はサイエンス、心理学、マーケティング、医学、など幅広い分野で利用されています。

私たちは、日々新たなデータ（事実）に晒されています。統計は、それらの膨大なデータを整理、要約し、データが持つ意味の解釈に基づいて何らかの結論を導きます。

統計は、データのサンプリング、分析、要約、解釈、などなど、データ分析のあらゆる作業に関わります。統計は「データ分析の肝」と言っても過言ではありません。

母集団とサンプル

統計の重要な概念、母集団: Populationとサンプル: Sampleの違いをまとめます。

母集団: Populationは、推定したい全体のグループを指します。

これに対し、サンプル: Sampleは、母集団から何らかの作法で収集（サンプリング: Sampling）して得た特定のグループです。サンプルは母集団のサブセットです。サンプルのサイズは、母集団のサイズより常に小さいです。

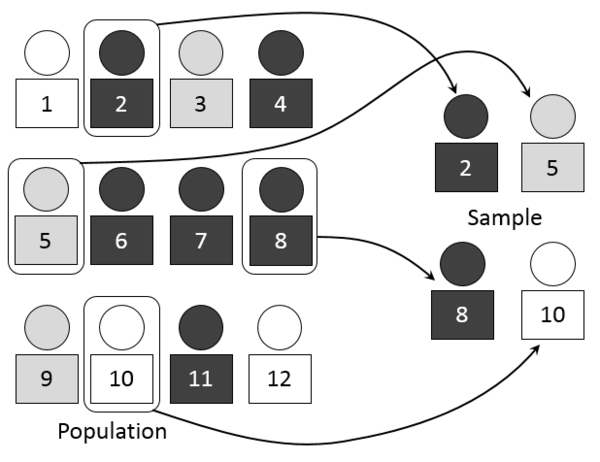
サンプルを利用する目的は何でしょう？

サンプルを利用することで、母集団の性質を推定するためです。

例えば、母集団を常に調査することは非現実的でコストがかかる課題があげられます。

一方、母集団からサンプリングして得たサンプルが、ランダムかつ十分な数であれば、より大きなサイズの母集団に関する推定が可能です。

母集団とサンプルの関係の一例として、消費者アンケートから他の購入者の意見を推定することがあげられます。

記述統計と推測統計

では、本題の記述統計と推測統計の違いについてまとめます。

記述統計

記述統計: Descriptive statisticsは、データセットの特徴を記述するために利用されます。

データの特徴を調べる記述統計手法には、(1)データの可視化、(2)統計量の計算があります。

メジャーな可視化手法として、データセットの分布を調べるヒストグラム、ボックスプロット、散布図があげられます。また、平均値、中央値、最頻値、標準偏差、相関係数、などが統計量としてあげられます。

記述統計は母集団、サンプルの両方に利用されます。

推測統計

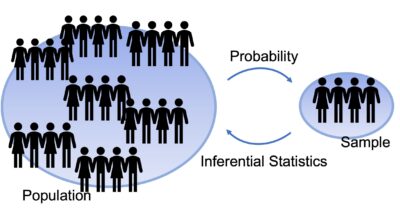
推測統計: Inferential statisticsは、母集団からサンプリングして得たサンプルの情報に基づいて、母集団を一般化するために利用されます。

推測統計において重要な手法に、点推定、仮説検定、信頼区間推定、があげられます。

推測統計は、データの特徴を知ることよりも、母集団を推定（予測）することに専念します。結果には、確率: Probabilityが扱われます。

まとめ

この記事は、記述統計と推測統計の違いについてまとめました。

教科書的な定義をまとめただけですが、母集団の定義、サンプリング方法、ベイズ統計などに関連する議論⁽³⁾を拝見していると、最終的に、統計の世界は奥が深く、もっと勉強しないと…という気持ちになったのでした。

この記事は以上です。最後まで読んで読んで頂きありがとうございました。

参考資料

(1) Wikipedia, Sampling (statistics)(2022/7/12アクセス)

(2) Jay L. Devore, kenneth N. Berk, Modern Mathematical Statistics with Application, Springer Science & Business Media, 2011

(3)「全数調査なら何でもわかる」という誤解 – 間違えがちな母集団とサンプリングそしてベイズ統計 – (2022/7/14 アクセス)