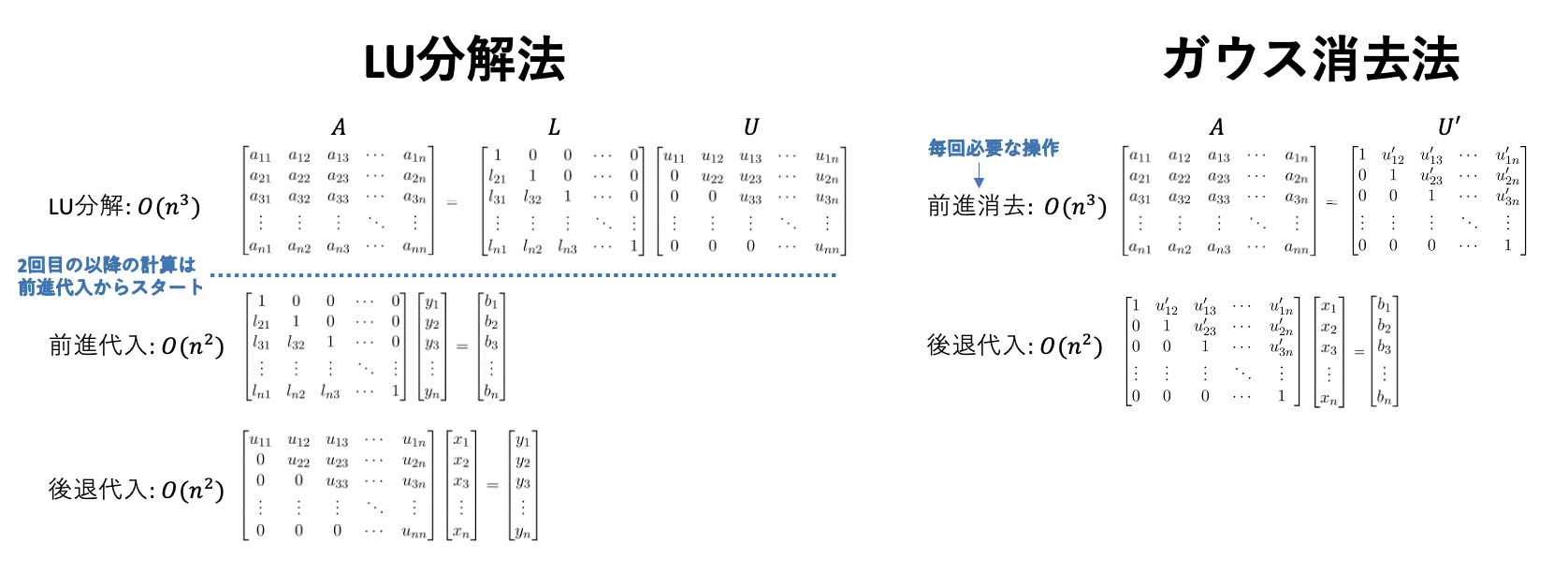
LU分解は、正方行列を下三角行列と上三角行列の積に分解する方法です。
LU分解を利用すれば、連立一次方程式の計算をさらに効率化できます。
- LU分解とは何か
- なぜLU分解が計算を効率化するのか
- LU分解とガウス消去法にどんな違いがあるのか
LU分解
LU分解(LU decomposition)は
$$A=LU$$
に分解する方法です。
\(A\)は正方行列(Square matrix)、\(L\)は下三角行列(Lower triangular matrix)、\(U\)は上三角行列(Upper triangular matrix)です。
\(A\)がn元連立一次方程式の係数行列とすると、それぞれの行列は
\(A = \begin{bmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\
a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\
a_{31} & a_{32} & a_{33}&\cdots & a_{3n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & a_{n3} &\cdots & a_{nn}
\end{bmatrix}\)
\(L = \begin{bmatrix}
1 & 0 & 0 &\cdots & 0 \\
l_{21} & 1 & 0 &\cdots & 0 \\
l_{31} & l_{32} & 1 &\cdots & 0 \\
\vdots & \vdots & \vdots &\ddots & \vdots \\
l_{n1} & l_{n2} & l_{n3} & \cdots & 1
\end{bmatrix}\)
\(U = \begin{bmatrix}
u_{11} & u_{12} & u_{13} &\cdots & u_{1n} \\
0 & u_{22} & u_{23} &\cdots & u_{2n} \\
0 & 0 & u_{33} &\cdots & u_{3n} \\
\vdots & \vdots & \vdots &\ddots & \vdots \\
0 & 0 & 0 & \cdots & u_{nn}
\end{bmatrix}\)
です。\(L\)の対角要素を1とおきます。

LU分解は1948年にアラン・マシスン・チューリング(Alan Mathison Turing)に考案されました。アラン・チューリングは、コンピュータの基礎・原理を築いた方です。アラン・チューリングがどんな人か興味があれば「映画: イミテーションゲーム」がオススメです。
LU分解を使った計算

\(A\boldsymbol{x}=\boldsymbol{b}\)を計算するために、LU分解をどのように利用するんでしょうか?
LU分解を使ったステップを書き出してみます。
- \(A\)をLU分解する
$$A\boldsymbol{x}=LU\boldsymbol{x}$$ - \(U\boldsymbol{x}=\boldsymbol{y}\)とおく
$$\begin{eqnarray}L(U\boldsymbol{x})&=&L\boldsymbol{y}\\
&=&\boldsymbol{b}\end{eqnarray}$$ - \(L\boldsymbol{y}=\boldsymbol{b}\)を使って\(\boldsymbol{y}\)を解く
- \(U\boldsymbol{x}=\boldsymbol{y}\)を使って\(\boldsymbol{x}\)を解く
\(\boldsymbol{x} =\begin{bmatrix}x_1\\x_2\\x_3\\\vdots\\x_n\end{bmatrix} \quad
\boldsymbol{y} =\begin{bmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{bmatrix} \quad
\boldsymbol{b} =\begin{bmatrix}b_1\\b_2\\b_3\\\vdots\\b_n\end{bmatrix} \quad\)とおきます。
まず、\(L\boldsymbol{y} = \boldsymbol{b}\)は、
$$\begin{bmatrix}
1 & 0 & 0 &\cdots & 0 \\
l_{21} & 1 & 0 &\cdots & 0 \\
l_{31} & l_{32} & 1 &\cdots & 0 \\
\vdots & \vdots & \vdots &\ddots & \vdots \\
l_{n1} & l_{n2} & l_{n3} & \cdots & 1
\end{bmatrix}
\begin{bmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{bmatrix}=\begin{bmatrix}b_1\\b_2\\b_3\\\vdots\\b_n\end{bmatrix}$$
です。これを\(y_1\)から\(y_n\)の順に解きます。
この操作を前進代入と呼びます。
その後、\(U\boldsymbol{x}=\boldsymbol{y}\)より
$$\begin{bmatrix}
u_{11} & u_{12} & u_{13} &\cdots & u_{1n} \\
0 & u_{22} & u_{23} &\cdots & u_{2n} \\
0 & 0 & u_{33} &\cdots & u_{3n} \\
\vdots & \vdots & \vdots &\ddots & \vdots \\
0 & 0 & 0 & \cdots & u_{nn}
\end{bmatrix}
\begin{bmatrix}x_1\\x_2\\x_3\\\vdots\\x_n\end{bmatrix}=
\begin{bmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{bmatrix}$$
です。\(x_n\)から\(x_1\)の順に解きます。
この操作を後退代入と呼びます。
この操作によって、\(\boldsymbol{x}\)が求められました。
LU分解とガウス消去法

LU分解を連立一次方程式に使うと何が良いのでしょうか?
LU分解を利用すれば、同じ係数を使って複数回の連立方程式を解く場合の計算量を減らせます。

なぜLU分解を利用すると計算量を減らせるのでしょうか?
前進代入と後退代入の操作だけで解を計算できるからです。
\(A\)をLU分解するための計算量は、\(O(n^3/3)\approx O(n^3)\)です。
一方、\(L、U\)は三角行列ですから、それぞれの代入操作によって解を求めるための計算量は\(O(n^2/2)\approx O(n^2)\)です。
1回目の計算量は、LU分解を実行する必要があるため、計算量はガウス消去法と同じ\(O(n^3)\)です。
しかし、同じ係数行列を使って、異なる\(\boldsymbol{b}\)に対して何度も解を計算する必要がある場合、すでに得られたL, Uを使えば、計算量は\(O(n^2)\)ですみます。
一方、ガウス消去法は\(\boldsymbol{b}\)が変わるたびに三角行列を作る必要があるため、計算量は常に\(O(n^3)\)です。
時間計算量の違い
アルゴリズムが問題を解くために実行する処理やステップの回数を時間計算量(time complexity)と呼びます。
時間計算量が小さいほど、コンピュータは短い時間で問題を解くことができます。

\(O(n^2)\)と\(O(n^3)\)の時間計算量は、大規模なデータを扱う場面で大きな違いが出ます。
下図は\(O(n^2)\)と\(O(n^3)\)の時間計算量の違いを示しています。
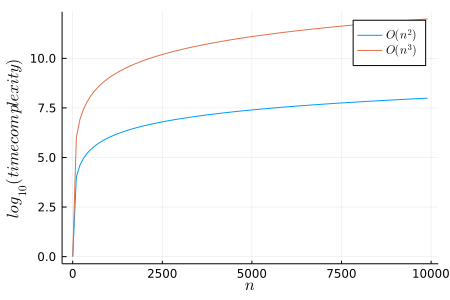
\(n\)が小さいとき、両者の時間計算量に大きな違いはありませんが、\(n\)が大きくなるにつれて差が現われます。
例えば、サイズが1万のデータを扱う場合、\(O(n^2)\)と\(O(n^3)\)の間には1万倍の時間計算量の違いが出ています。
\(O(n^2)\)のアルゴリズムが10秒で終える計算を、\(O(n^3)\)のアルゴリズムはおよそ27.8時間かけると見積れます。
LU分解の実装
最後にJuliaを使ってLU分解を実装してみます。
sol_L()は前進代入、sol_U()は後退代入を実行します。sol_LU()はLU分解を利用して解を計算します。lu()は正方行列に対してLU分解を実行します。

sol_LU(A, b)とA\bの差がほぼ0なので、同じ解が得られているようですね。
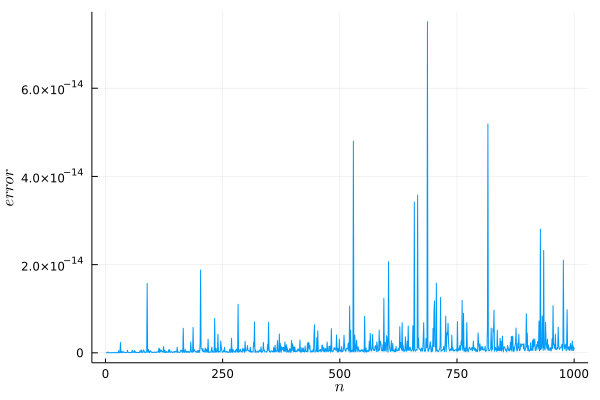

Juliaで\はLU分解を適用しています。
まとめ
- LU分解は\(A\)を下三角行列\(L\)と上三角行列\(U\)の積に分解
- LU分解の時間計算量は\(O(n^3)\)、前進代入、後退代入はそれぞれ\(O(n^2)\)
- 複数回解を計算する必要がある場合、LU分解は計算量を効率化
- Juliaのバックスラッシュ
\でもLU分解は使える

今回のお話で計算量をなぜ意識すべきか分かった気がしました!
以上です。最後まで読んで頂きありがとうございました。
参考文献
(1): Julia, “Linear Algebra” (6/27/2021アクセス)













この記事は「LU分解」についてまとめます。