高校・大学で学ぶテイラー展開は、機械学習でも利用されています。
テイラー展開は、無限級数を利用することで、任意の関数のある点近傍の値を近似します。この性質は、複雑な関数の周辺情報を獲得することに役立ちます。
- テイラー展開とは何か?
- テイラー展開はどのような性質か?
- 機械学習でテイラー展開がどのように利用されるか?
テイラー展開
テイラー展開(Taylor series)は
- \(f(x)\)が点\(c\)を含む区間で無限回微分可能な関数
- \(n \to \infty\)のときテイラーの定理における剰余項が\(0\)に収束
を満たすとき、点\(c\)を基準とした周辺の値は、以下の多項式に近似できます。


機械学習でテイラー展開を利用すると何が嬉しいんでしょうか?
テイラー展開のメリットは、多項式近似による1)複雑な計算の簡略化、2)任意の点\(c\)周辺情報の獲得、です。
例えば、機械学習においては、ある機械学習モデルの損失関数(\(L(x)\))の計算を単純にするためにテイラー展開を利用します。
テイラー展開の特徴を可視化

うーん、文章と式だけではまだ理解できないです…
Juliaを使ってテイラー展開の特徴を可視化してみます。
例えば、\(f(x)=e^x\)において、\(c=2\)を基準とした周辺の情報を知りたいとします。
このとき、一次近似、二次近似、、、、n次近似はそれぞれ
\( \vdots \)
です。
これを可視化したものが下のアニメーションになります。
テイラー展開の項の数が増えるにしたがって、\(P(x)\)で\(c=2\)を基準とした周辺の値を近似していることが確認できます。
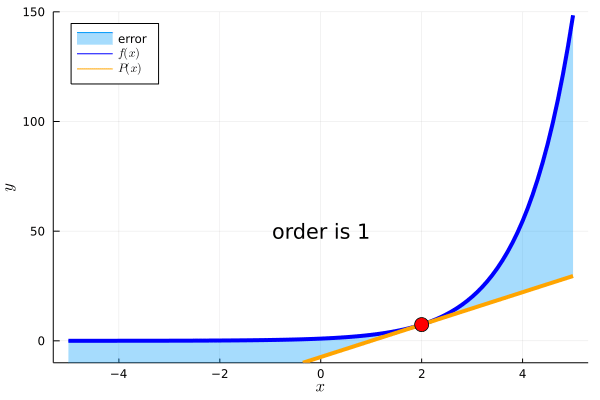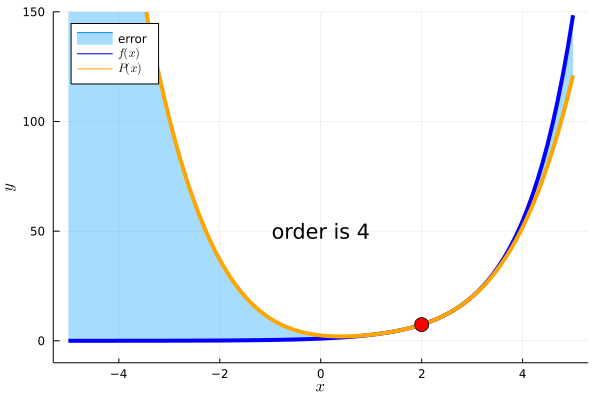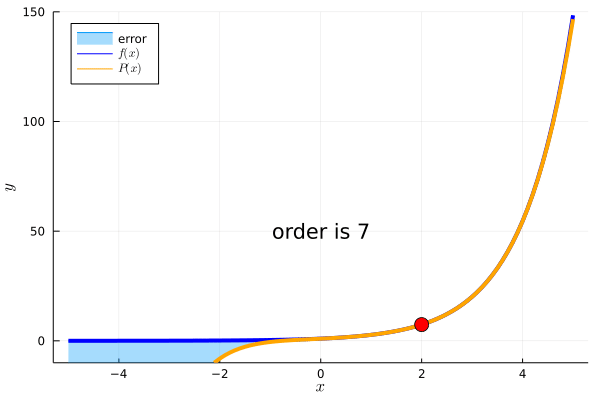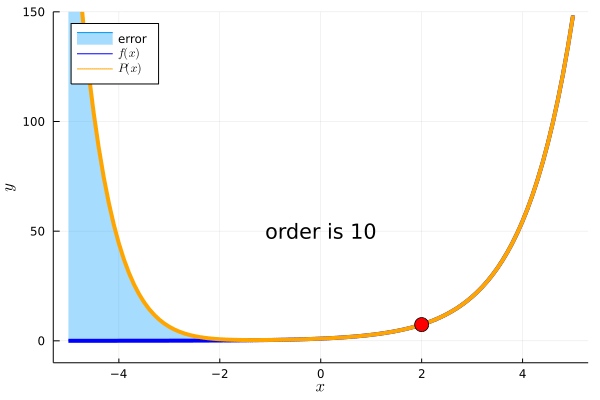
以下はアニメーションを作るためのJuliaのコードです。TaylorSeriesは、Juliaでテイラー展開を扱うパッケージです。
\(f(x)=cos(x)\)において、\(c=0\)を基準とした周辺の情報を知りたいときも同様です。6次近似すれば、\(c=0\)を基準に\(-2\leq x \leq 2\)の範囲を\(P(x)\)で計算できます。
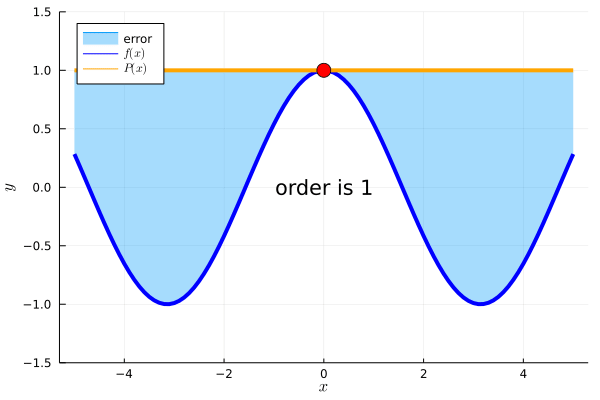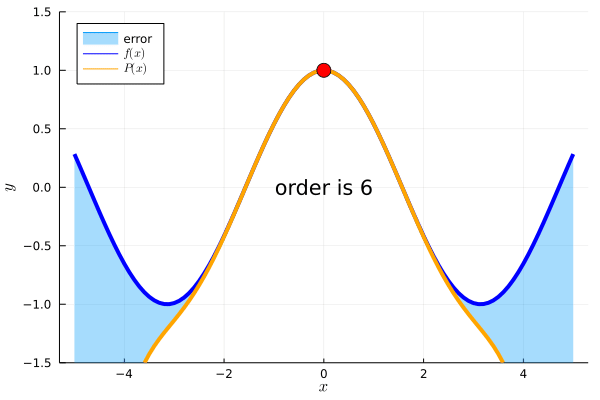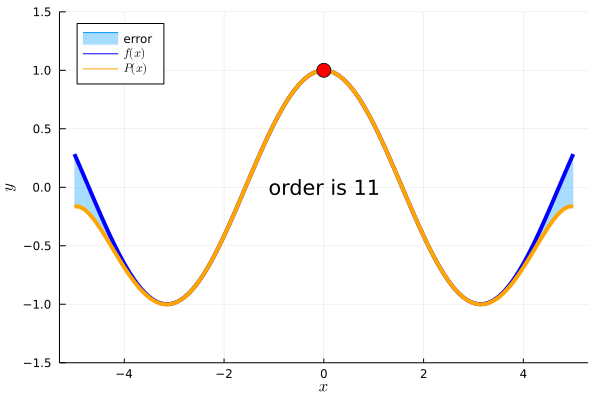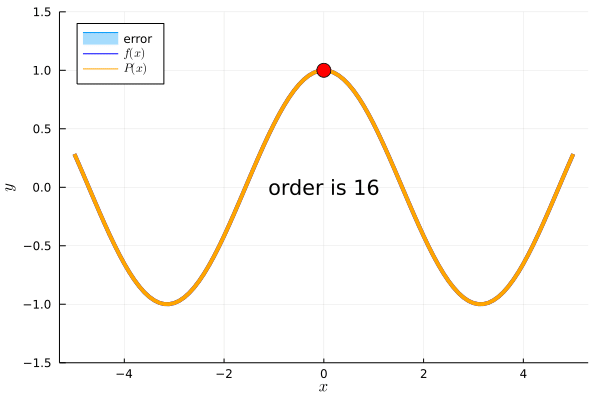

なるほど!テイラー展開の項の数が増えるほど、基準点を中心に\(P(x)\)から\(f(x)\)を計算できるということですね!

その通りです。より詳しくは「3Blue1Brown」の動画もオススメです。
まとめ
- テイラー展開は複雑な関数を多項式近似する \(f(x)\approx P(x)\)
- テイラー展開は、1)複雑な計算の簡略化、2)任意の点(\(c\))の周辺情報の獲得に役立つ
- 機械学習では損失関数の計算に利用される

多くの方が高校・大学数学でテイラー展開を勉強したけど、暗記だけで終わったのではないでしょうか。式の可視化方法、動画の無料公開、などがあり、ほんと便利な時代になったなぁと思います。
この記事は以上です。最後まで読んで頂きありがとうございました。
参考資料
(1): James D. McCaffrey, “The Taylor Series and Machine Learning”, August 30, 2017
(2): Blake Sanie, towards data science, “Computing PI in Only 3 Lines”, December 22, 2020
(3): Shahbaz KhanShahbaz Khan, toward data science, “Mathematical Intuition behind Gradient Descent”, May 8, 2019
(4): TaylorSeries.jl, Userguide v0.11.2 (7/14/2021アクセス)





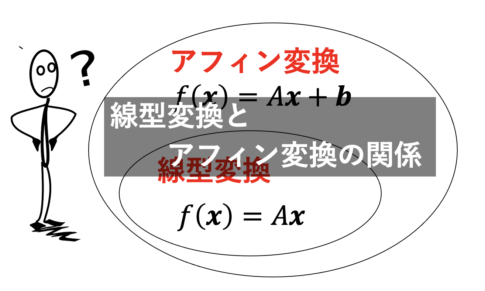







この記事は「テイラー展開の性質」についてまとめます。