Juliaと遊ぶ線形代数(5) ガウス・ジョルダン消去法とガウス消去法の比較

ガウス・ジョルダン消去法、ガウス消去法は、連立一次方程式を解くための手法です。

学校の試験では、多くの人が連立一次方程式を自力で計算しています。

しかし、理工系の科学計算では、数百万以上におよぶ大規模な連立一次方程式を扱う場面があります。そのような規模の問題を解くためには、必ずコンピュータを利用します。

そして、問題を効率的に解くために計算量を考慮する必要があります。

この記事は「ガウス・ジョルダン消去法」と「ガウス消去法」についてまとめます。

背景

なぜ「ガウス・ジョルダン消去法」や「ガウス消去法」が必要なのでしょうか？

高校で学ぶ\(A^{-1}\)を利用した逆行列法は、大規模な数値計算になると時間がかかるからです。

逆行列の計算は「クラメルの公式」を使っています。しかし、この公式の計算量は大きいです。

したがって、特別な理由がない限りは逆行列法は避けるべきと言えます。

逆行列法に比べ、ガウス・ジョルダン消去法、ガウス消去法は、効率的な計算を行う基本手法です。

さらに効率的な計算手法にLU分解が登場してきますが、LU分解のコンセプトを理解するためにもガウス消去法は大事です。

ガウス・ジョルダン消去法

ガウス・ジョルダン消去法は、以下のステップから係数拡大行列の係数行列部分を単位行列に変形することで解を得ます。

最大の絶対値を持つ行を選択し、行を入れ替える操作を「ピボット選択」と呼びます。

ガウス・ジョルダン消去法(Gauss-Jordan elimination)は「行列の基本変形」とも呼ばれます。

\[\left\{
\begin{array}{rcrcrc@{\qquad}l}
x_1 & + & x_2 &+& x_3= &3\\
4x_1 & + & 3x_2 &+& 2x_3= &8\\
9x_1 & + & 3x_2 &+& 4x_3= &7\\
\end{array}
\right.\]

は行列を使って

$$\begin{bmatrix}
1&1&1\\
4&3&2\\
9&3&4
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix} =
\begin{bmatrix}
3\\
8\\
7
\end{bmatrix}$$

と表せます。これを拡大係数行列にします。

$$
\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
4 & 3 & 2 & 8 \\
9 & 3 & 4 & 7
\end{array}\right]
$$

実際に拡大係数行列を\(\begin{bmatrix}{A|\boldsymbol{b}}
\end{bmatrix} \longmapsto
\begin{bmatrix}{E|A^{-1}\boldsymbol{b}}
\end{bmatrix}\)に変形してみます。

$$
\begin{aligned}
\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
4 & 3 & 2 & 8\\
9 & 3 & 4 & 7
\end{array}\right] &\longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
9 & 3 & 4 & 7
\end{array}\right] \\
&\longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 6 & 5 & 20
\end{array}\right] \\
& \longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 0 & 7 & 4
\end{array}\right]\\
& \longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 0 & 1 & 4/7
\end{array}\right]\\
&\longmapsto\left[\begin{array}{ccc|c}
1 & 0 & -1 & -1 \\
0 & 1 & 2 & 4 \\
0 & 0 & 1 & 4/7
\end{array}\right] \\
& \longmapsto\left[\begin{array}{ccc|c}
1 & 0 & 0 & -3/7 \\
0 & 1 & 2 & 4 \\
0 & 0 & 1 & 4/7
\end{array}\right]\\
& \longmapsto\left[\begin{array}{ccc|c}
1 & 0 & 0 & -3/7 \\
0 & 1 & 0 & 20/7 \\
0 & 0 & 1 & 4/7
\end{array}\right]
\end{aligned}
$$

単位行列に変形することで、\(\boldsymbol{x}=[-\dfrac{3}{7} \quad \dfrac{20}{7} \quad \dfrac{4}{7}]^T\)が得られました。

ガウス消去法

ガウス消去法(Gaussian elimination)は、同様のステップで拡大係数行列を行階段形(row echelon form)に変形して解を得ます。

ガウス消去法は「掃き出し法」とも呼ばれます。

拡大係数行列は

$$
\begin{aligned}
\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
4 & 3 & 2 & 8\\
9 & 3 & 4 & 7
\end{array}\right] & \longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
9 & 3 & 4 & 7
\end{array}\right] \\
& \longmapsto\left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 6 & 5 & 20
\end{array}\right] \\
&\longmapsto \left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 0 & 7 & 4
\end{array}\right]\\
&\longmapsto \left[\begin{array}{ccc|c}
1 & 1 & 1 & 3 \\
0 & 1 & 2 & 4 \\
0 & 0 & 1 & 4/7
\end{array}\right]
\end{aligned}
$$

に変形できます。ここまでの操作を前進消去(forward elimination)といいます。

変形した拡大係数行列を連立方程式で表すと

\[\left\{
\begin{array}{rcrcrc@{\qquad}l}
x_1 & + & x_2 &+& x_3= &3\\
&& x_2 &+& 2x_3 = &4\\
&& && x_3= &4/7\\
\end{array}
\right.\]

です。これは

\[\left\{
\begin{array}{rcrcrc@{\qquad}l}
x_1 &= &3-x_2-x_3\\
x_2 &= &4 -2x_3\\
x_3 &= &4/7\\
\end{array}
\right.
\]

とおけます。\(x_3\)から\(x_1\)の順に解きます。この操作を後退代入(backward substitution)と呼びます。

ガウス消去法は、(1)前進消去で行階段形を作り、(2)後退代入で下からドミノ倒し的に解を得ます。

「ガウス・ジョルダン消去法」と「ガウス消去法」の比較

やってることが同じに思えるのですが、２つの方法にどんな違いがあるんでしょう？

計算量に違いがでます。係数行列のサイズを\(N \times N\)とすると、ガウス・ジョルダン消去法の計算量はおよそ\(O(N^3/2)\)、ガウス消去法の計算量はおよそ\(O(N^3/3)\)です。

したがって、ガウス・ジョルダン消去法の計算量は、ガウス消去法の計算量より大きいと予想できます。同じコンピュータで同じ問題を解いても、計算量が大きいと計算終了までに長い時間がかかります。

実際に比較してみます。(このコードはピボット選択を含んでいません)

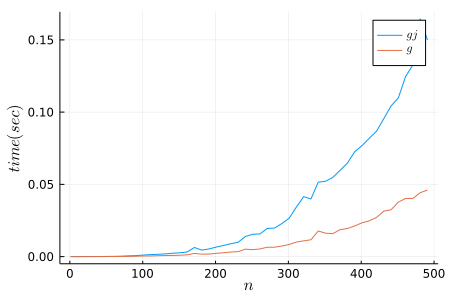
両者の計算時間を比較したところ、ガウス消去法はガウス・ジョルダン消去法より計算効率が良いと確認できました。

この結果から、(1)アルゴリズムで計算量が変わる、(2)計算量の大きさが計算時間に影響する、ことがわかりました。

まとめ

同じ問題を解いているのに、解き方で計算時間が変わるって面白いですね。

紙の上だけではなく、コンピュータを動かしながら線形代数の勉強をしてみると、線形代数の理解が深まって良いと思います。

次回はLU分解についてまとめます。最後まで読んで頂きありがとうございました。

参考文献

(1): Treee July, “Numerical Analysis by Julia Series 1-Gauss Elimination” (6/24/2021アクセス)

(2): MIT, Gaussian-elimination, 9/23/2017

(3): 桂田 祐史, 連立1次方程式 I, — 計算量と直接法 —, 3/23/2018