ブートストラップ法は、データセットから無作為に何度もリサンプリングして母集団の特徴の推定を試みる統計手法です。
複雑な計算を簡単なシミュレーションに置き換えたブートストラップ法は、今日ではコンピュータ技術の発展に伴い、よりパワフルで扱いやすい手法となりました。
ブートストラップ法
関連用語
まずブートストラップ法に関連して、定義を明確にしておきたい用語です。
- 母集団(population): 調査対象とする集合全体。多くのケースで母集団を完全に把握することは不可能。
- サンプル(sample): 母集団から抽出したデータの集合。データセット、標本とも呼ぶ。
- サンプリング(sampling): 母集団の特徴を推定するために、巨大なデータの集合(データセット)から一部データを抽出してサブセットを作成する操作。
- 復元抽出 (sampling with replacement): データセットから一度抽出したデータを再び抽出対象とするサンプリング手法。
特徴
ブートストラップ法: Bootstrap methodは、擬似母集団と見立てたデータセットから復元抽出を何度も行うことで多数のサブサンプルを作成し、その後、得たサブサンプルを使って母集団の平均、標準偏差、信頼区間などの統計量を推定する方法です。
Figure1はブートストラップ法のコンセプト図を示します。
ここでは、\(\mathbf{Z}\): \(N\)個のサンプル\(z_i = (x_i, y_i)\)を含むデータセット、\(\mathbf{Z}^{*b}\): \(b\)回目の復元抽出から得たサブサンプル、\(S(\mathbf{Z})\): \(\mathbf{Z}\)から得られる統計量、とおきます。
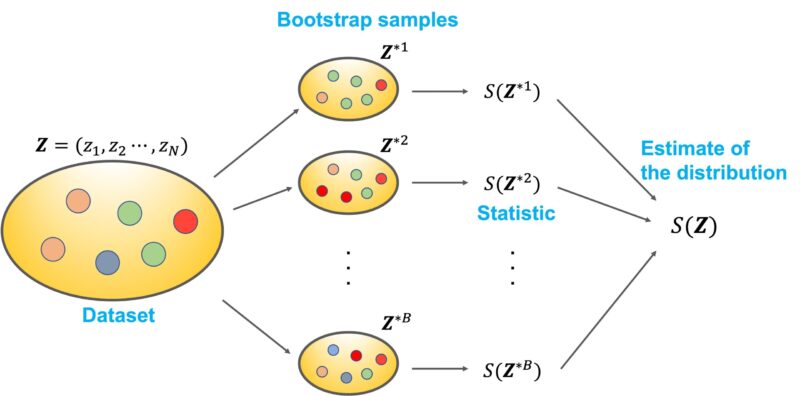
ブートストラップ法は以下のステップを経て、母集団を推定します。
- データセットから作成するサブセットの数\(B\)を決定
- データセットから\(N\)個のサンプルを復元抽出
- サブセットの統計量\(S(\mathbf{Z}^{*b}), b\in B\)を計算
- (2),(3)の操作を\(B\)回反復
- \(B\)個のサブサンプルの統計量から母集団の統計量を推定
例えば、ブートストラップ法から得られる母集団の平均\(\bar{S^*}\)は
$$\bar{S}^*=\frac{1}{B}\sum^{B}_{b=1} S(\mathbf{Z}^{*b})$$
ブートストラップ法から得られる母集団の分散\(\hat{Var}(S(\mathbf{Z}))\)は
$$\hat{Var}[S(\mathbf{Z})]=\frac{1}{B-1}\sum^B_{b=1}(S(\mathbf{Z}^{*b})-\bar{S}^*)^2$$
となります。

この記事では割愛しますが、ブートストラップ法と類似した手法にジャックナイフ法があります。
利用する場面

ブートストラップ法はどのような場面で利用するのでしょう?
ブートストラップ法は、母集団が正規分布と仮定できない場合に利用します。
例えば、母集団の信頼区間を求めたいとき、伝統的な統計学ではt-検定を利用します。しかしながら、t-検定を利用するには母集団が正規分布と仮定する必要があります。実際の母集団が常に正規分布とは保証されません。
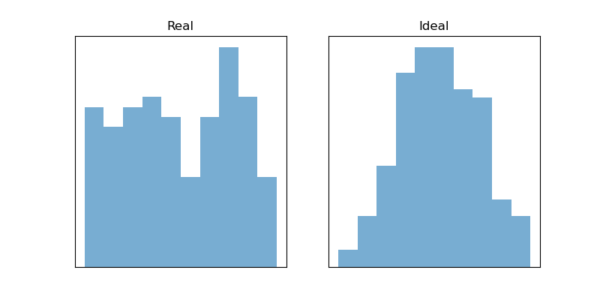
このように母集団が正規分布か不明なとき、ブートストラップ法は、サンプルを母集団の性質を反映している擬似母集団と見立て、何度も擬似母集団からサンプリングして母集団の統計量を推定します。
気をつけたい点
一見便利そうに思えるブートストラップ法ですが、弱点もあります(4)。ここでは、ブートストラップ法の長所と短所をまとめます。
- 複雑な分布に対する誤差、信頼区間などの統計量の推定方法がシンプル
- 結果の安定性を確認に優れた手法
- 正規分布を仮定して得た信頼区間よりも精度が高い
- 信頼区間が本当に正しいか判断できない
- 結果が代表的なサンプルに依存する
ブートストラップ法を利用する場合、オリジナルのサンプルサイズは大きい方が好ましいとされます。
繰り返しになりますが、ブートストラップ法は、サンプルを母集団と見立て、リサンプリングを通して母集団の特徴を推定する手法です。
しかし、もしサンプルが母集団の特徴と大きく異なるものならば、ブートストラップ法の前提条件自体が誤りであり、ブートストラップ法からの推定結果は実際の母集団と異なるものとなります。

比較的少ないデータ数から母集団を推定するとはいえ、データが少なすぎても問題があるみたいですね。
ブートストラップ法の挙動
最後に、リサンプリングの回数\(B\)が大きくなるにつれ、ブートストラップ法から推定する平均、分散がどのように変化するか確認してみます。
今回、「20代男性サラリーマンがお財布に入れている現金の推定」を例としてみます。
まず、東京駅前で150名のサラリーマンにアンケートを実施しました。得られたデータを可視化してみると、正規分布でないことが分かりました (Figure3)。そこで、ブートストラップ法を利用することにしました。
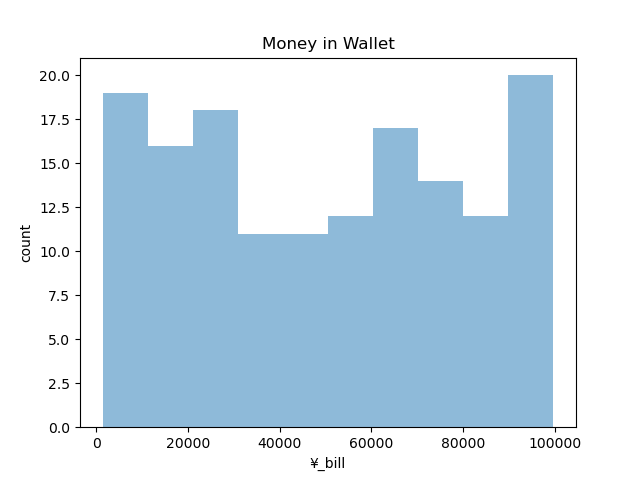
Figure3のデータセットに対してリサンプリングを最大300回実施しました。\(b \in B, \quad b=2,\cdots 300\)

リサンプリングの回数に応じて、平均と分散はどのように変化するんでしょう。
Figure4は、リサンプリングの回数\(B\)とブートストラップサンプルから得られる平均・分散の関係を示します。
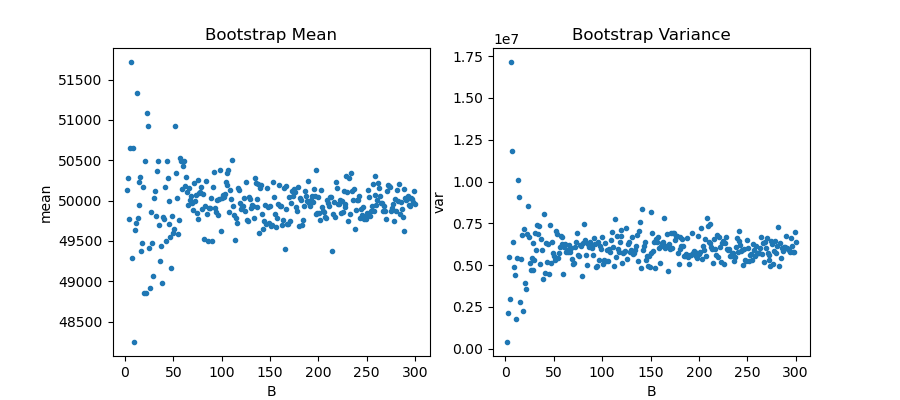
リサンプリング回数\(B\)が小さいとき、得られる平均・分散の値は大きくバラついていましたが、\(B>60\)あたりから平均、分散のバラツキが収束していることが確認できます。
Figure5は、リサンプリング回数\(B\)が大きくなったときのブートストラップ方によって推定する平均と95%信頼区間の変動を示します。
\(B\)の値が大きくなるにつれ、ブートストラップサンプリングから得られる平均値も収束していくことが確認できます。このデータセットについては\(B=100\)あたりで十分そうです。
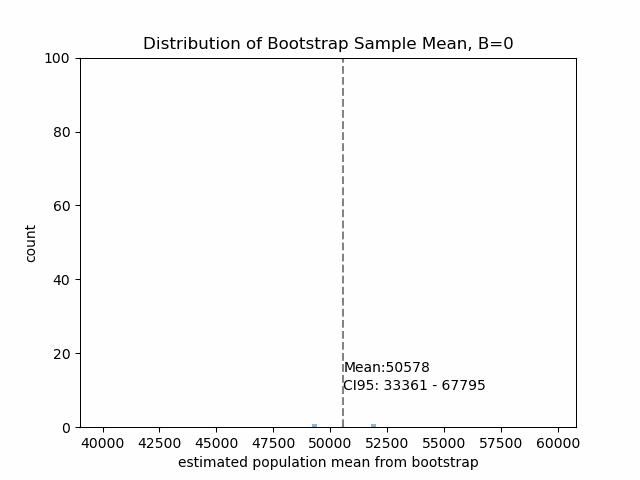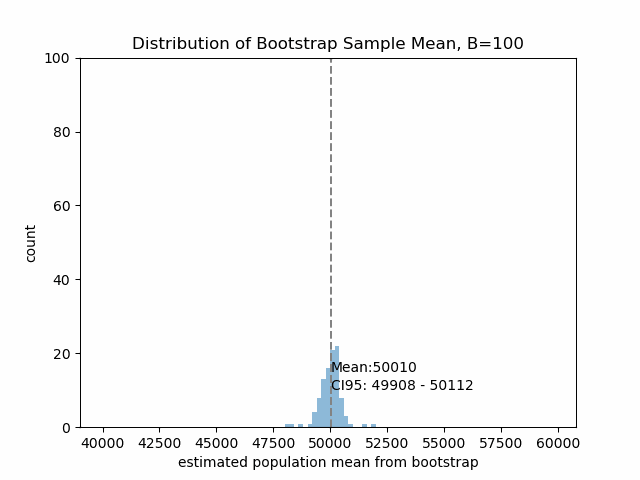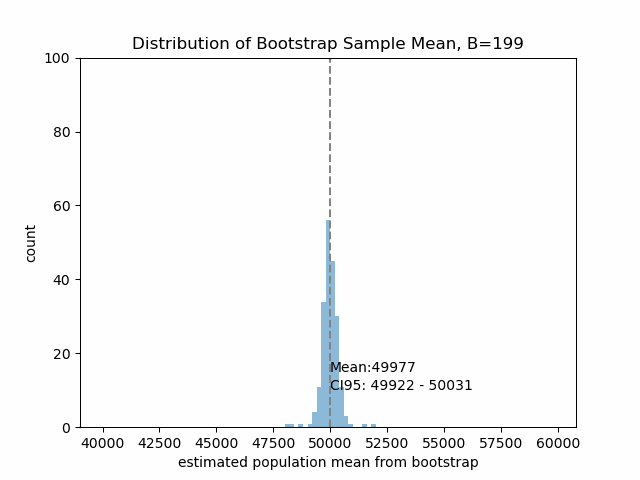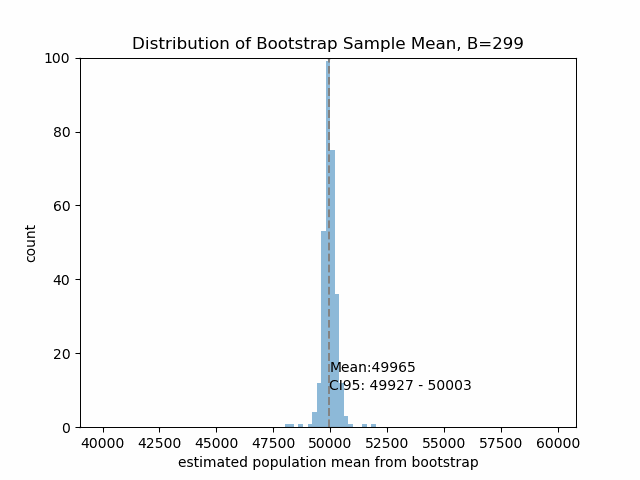

ブートストラップ法から、母集団平均は5万円ほどと推定されるわけですね!
まとめ
この記事はブートストラップ法についてまとめました。
- 特徴
- サンプルを無作為に何度もリサンプリングし、母集団の特徴の推定を試みる統計手法
- サンプルは母集団の性質を反映していることを前提とする
- 母集団が正規分布ではない場合に利用
- 長所
- 複雑な分布に対する誤差、信頼区間などの統計量の推定方法がシンプル
- 結果の安定性を確認に優れた手法
- 正規分布を仮定して得た信頼区間よりも高精度
- 短所
- 信頼区間が本当に正しいか判断困難
- 結果が代表的なサンプルに依存

機械学習モデルにおいて、ブートストラップ法はバギング(bagging)と呼ばれる手法で扱われています。バギングは、RandomForest、AdaBoost、GradientBoost、XGBoostなど、多くのアンサンブル学習モデルで利用される手法です。
この記事は以上です。最後まで読んで頂きありがとうございました。
参考資料
(1) Trevor Hastie, Robert Tibshirani, Jerome Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2009
(2) Dirk P. Kroese, Zdravko Botev, Thomas Taimre, Radislav Vaisman, Data Science and Machine Learning: Mathematical and Statistical Methods, 2020
(3) Jay L. Devore, Kenneth N. Berk, Modern Mathematical Statistics with Applications, 2011
(4) Wikipedia,Bootstrapping (statistics) (2022/7/28アクセス)
(5) A Gentle Introduction to the Bootstrap Method (2022/7/20アクセス)














この記事は「ブートストラップ法」についてまとめます。