コーシー・シュワルツの不等式はベクトルの内積とノルムの関係を、三角不等式は三角形の2辺の和の長さが残りの1辺の長さより必ず大きくなることを示します。
- コーシー・シュワルツの不等式の証明
- 三角不等式の証明
コーシー・シュワルツの不等式
コーシー・シュワルツの不等式(Cauchy-Schwarz inequality)は、ノルムと内積の関係を示します。
$$|a^T b|\leq ||a||||b||$$
これをn-vectorとして展開すると、
$$|a_1b_1+…+a_n b_n|\leq (a_1^2+…+a_n^2)^{1/2} (b_1^2+…+b_n^2)^{1/2}$$
とも書けます。
$$
\begin{aligned}
0 &\leq||\beta a-\alpha b||^{2} \\
&=||\beta a||^{2}-2(\beta a)^{T}(\alpha b)+||\alpha b||^{2} \\
&=\beta^{2}||a||^{2}-2 \beta \alpha\left(a^{T} b\right)+\alpha^{2}||b||^{2} \\
&=||b||^{2}||a||^{2}-2||b||||a||\left(a^{T} b\right)+||a||^{2}||b||^{2} \\
&=2||a||^{2}||b||^{2}-2||a||||b||\left(a^{T} b\right)
\end{aligned}
$$
となる。これを\(2||a|||b|||\)で割ることで、
\(a^T b \leq ||a||||b||\)が導かれる。これと同じ操作を\(-a\)と\(b\)に対して行うと、\(-a^T b \leq ||a||||b||\)が得られる。
これらふたつの不等式より、最終的に
$$|a^T b|\leq ||a||||b||$$
が得られる。
- \(\beta a = \alpha b\)
- \(a = 0 \quad or \quad b =0\)
1の場合、いづれかのベクトルがもう一方のベクトルをスカラー倍したものであることが分かります。
三角不等式
三角不等式(Triangle inequality)はノルムの関係を示します。
$$||a+b|| \leq ||a||+||b||$$
三角不等式はコーシー・シュワルツの不等式を使って導くことができます。
\(\begin{aligned}||a+b||^2 &= ||a||^2+2a^T b+||b||^2\\
&\leq ||a||^2+2||a||||b||+||b||^2\\
&= (||a||+||b||)^2
\end{aligned}\)
したがって、\(||a+b|| \leq ||a||+||b||\)が成り立つ。

Youtubeの動画で視覚的に理解するのも手です。自分に合った動画を見つけてみてください。
Juliaで確認
最後に3-vectorを使って、両式の成立を確認します。
ソースコード中のresultは\(a, b\)を使った(右辺)-(左辺)の結果です。
resultsはresultを10万回繰り返して得たものです。
\(a, b\)の値は繰り返しのたびにランダムに変更されます。resultsが0未満をひとつも含まなければ、式が成立していると言えます。
コーシー・シュワルツの不等式
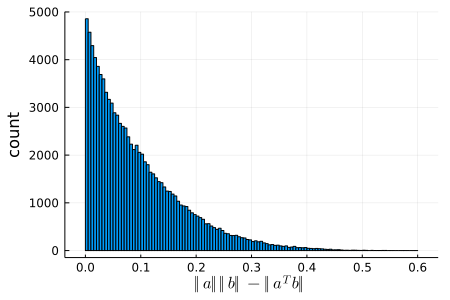
三角不等式


両式ともに0未満を含んでいないですね!成立!

JuliaのコードはPythonに似てるようで、for文の書き方も微妙に違います。要素の番号もRと同じくJuliaは1からスタートします。
まとめ
この記事をまとめます。
- コーシー・シュワルツの不等式はノルムと内積の関係を示す
- 三角不等式はコーシーシュワルツの不等式を使って求めることができる
以上です。最後まで読んで頂き、ありがとうございました。
参考文献










この記事は「コーシー・シュワルツの不等式」と「三角不等式」についてまとめます。