線形代数に関するトピックをまとめます.
統計・線形代数線形代数の基礎: 射影と最小二乗法の理解
線形代数で扱う射影は、高次元のデータセットに対する様々な数学演算の理解に役立ちます。 機械学習、数値計算において、射影の代表的な利用例には線形回帰、特異値分解などがあげられ、その利用は幅広いです。 射影がどのように利用さ...
LA
統計・線形代数
統計・線形代数Juliaと遊ぶ線形代数(7) グラム・シュミット・アルゴリズム
グラム・シュミット・アルゴリズム(Gram-Schmidt Algorithm)は、有限の線形独立なベクトルを取ったとき、これらのベクトルが張る部分空間と同じ部分空間を張るための正規直交系を作り出します。 この記事は「グ...
統計・線形代数線形代数学の基本定理:４つの基本部分空間
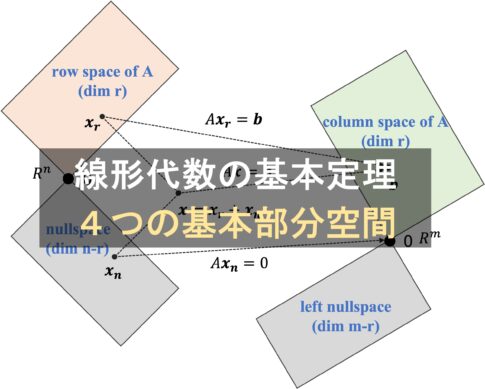
４つの基本部分空間(Four Fundamental Subspace)は、1993年にGilbert Strang氏の論文: “The fundamental theorem of linear algebra”&nb...
統計・線形代数線形代数の基礎: 線形独立と線形従属の違い
ある条件を満たすと、線形結合に扱われるベクトルは、線形独立、または、線形従属と呼ばれます。線形独立・線形従属は、他のベクトルと任意のスカラーで対象とするベクトルを表現できるか否かを示します。 この記事は復習のために「線形...
統計・線形代数線形代数の基礎: ベクトル空間とは何か？
ベクトル空間。高校・大学で線形代数を勉強したことはあるけど、私はすっかり忘れていました。概念が抽象的で同じように忘れている人も多いのではないでしょうか。 この記事は、復習のため、最低限知っておきたい「ベクトル空間」をまと...
統計・線形代数変換と行列：線形変換とアフィン変換の関係
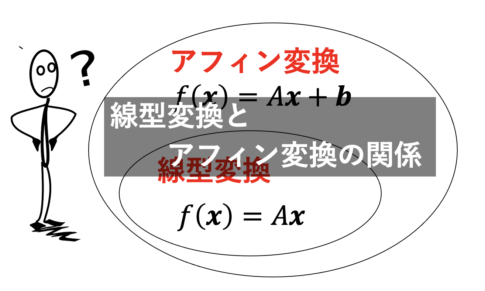
線形代数における線形変換とは何か？ 行列(マトリックス)を扱う線形代数は抽象度が高いうえ、３次元以上の可視化ができないため、海外の学生も理解に苦労していました。 この記事は、変換と行列の関係に注目して「線形変換とアフィン...
統計・線形代数機械学習とテイラー展開。機械学習で扱う数学的概念
高校・大学で学ぶテイラー展開は、機械学習でも利用されています。 テイラー展開は、無限級数を利用することで、任意の関数のある点近傍の値を近似します。この性質は、複雑な関数の周辺情報を獲得することに役立ちます。 この記事は「...
統計・線形代数Juliaと遊ぶ線形代数(6) LU分解とガウス消去法
LU分解は、正方行列を下三角行列と上三角行列の積に分解する方法です。 LU分解を利用すれば、連立一次方程式の計算をさらに効率化できます。 この記事は「LU分解」についてまとめます。 LU分解とは何か なぜLU分解が計算を...
統計・線形代数Juliaと遊ぶ線形代数(5) ガウス・ジョルダン消去法とガウス消去法の比較
ガウス・ジョルダン消去法、ガウス消去法は、連立一次方程式を解くための手法です。 学校の試験では、多くの人が連立一次方程式を自力で計算しています。 しかし、理工系の科学計算では、数百万以上におよぶ大規模な連立一次方程式を扱...
統計・線形代数Juliaと遊ぶ線形代数(4) 線形方程式
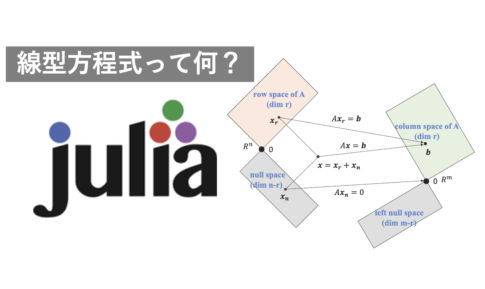
ビッグデータのような大規模データを扱うため、線形代数に関する知識・スキルが必要になります。 10年以上前に大学で線形代数を履修しましたが、その後、所属した化学系研究分野では、線形代数を利用する機会は皆無でした。 理系卒と...
Profile – プロフィール
Sponsored Links – スポンサーリンク
