便利なライブラリ、パッケージのおかげで、データ解析は簡単に実行できる状況になっています。
しかし、semester2の「Mathmatics for Data Science」履修後に、「線形代数をもっと理解することで得られる気づきがあるのではないか?」とも考えるようになりました。
- ベクトルとは何か
- ベクトルはどのように利用されているか
- Juliaでベクトルはどのように扱うか
ベクトル
定義
ここではベクトルを1次元配列、数が有限に並んだリストとして扱います。
分野によって説明が異なるため、ちゃんと引用しとくと以下。
ベクトル空間の元。線形性を持つ、すなわち和とスカラー倍を取ることができる量。
幾何学的空間における、大きさと向きを持った量。有向線分として捉えることができる。
Wikipedia, ‘ベクトル’
ベクトルは
$$v_1=\begin{bmatrix}
1 \\
2 \\
3 \\
\end{bmatrix} \quad or \quad
\begin{pmatrix}
1 \\
2 \\
3 \\
\end{pmatrix}
\quad or \quad (1, 2, 3)$$
と書けます。書き方に違いがありますが、どの表記も意味は同じです。
ベクトルの中に含まれるひとつひとつの値を要素(element)と呼びます。
ベクトルに含まれる要素の数をベクトルのサイズ(size)、あるいは、次元(dimension)と呼びます。
\(v_1\)は要素を3つ含んでいます。したがって、\(v_1\)のサイズ(次元)は3です。この場合、\(v_1\)は3-vectorと呼ばれます。
ベクトルの利用


ベクトルといえば、高校・大学のときに物理の力学で使いましたが、数学はとにかく計算だった気がします。実生活でベクトルはどんなことに利用されているんですか?
数例あげますと、
- 位置情報:2次元の位置情報だと2-vector(緯度、経度)、高度を含む3次元の場合は3-vector(緯度、経度、高度)が利用されます。
- 色:RGB表色系では、色は3-vector(赤、緑、青)で表されます。それぞれの要素は0-255の範囲の値を取り、色の違いはベクトル表現できます。
- 時系列:例えば、ある患者の心電図の記録をn-vector \((t_1, t_2, …,t_n)\)として扱えます。ある企業の株価やセンサーから得られるデータも同様です。
- 画像:画像が\(X \times Y\)ピクセルの画像の場合、その画像は\((X \times Y)\)-vector \((x_1, …, x_{X \times Y})\)で扱えます。
- 購入記録:あるユーザーの商品購入記録をn-vector \((p_1, p_2, …,p_n)\)として扱えます。2人のユーザーのベクトルを使えば、ユーザー同士がどれぐらい似た購入傾向であるかを判断できます。
- ワードカウント:ある記事で使用された単語の数はn-vector \((w_1, w_2, …,w_n)\)で表せます。
です。このように様々な用途に対してベクトルが利用されています。
ベクトルの足し算・引き算・掛け算
ベクトルの性質をまとめます。
ここで覚えておきたいことは
- ベクトルの次元が同じとき、数と同じようにベクトルも足し算・引き算ができる
- 逆に、次元が異なる2-vectorと3-vectorの足し算、引き算はできない
- ベクトルとスカラー(1-vector)は掛け算できる
ことです。

式としては以下の関係が成立します。\(\alpha, \beta, \gamma\)はスカラーです。(スカラー:ベクトルを定数倍する実数)
- \(a+b = b+a\)
- \((a-b)+c = a+(-b+c)\)
- \(\alpha a = a \alpha\)
- \((\beta \gamma) a = \beta (\gamma a)\)
- \((\beta + \gamma) a = \beta a + \gamma a\)
- \(\beta (a + b) = \beta a + \beta b\)
内積: Inner product
内積(Inner product)は
$$a^T b = a_1b_1 + a_2b_2 + …+a_n b_n$$
であり、2つのn-vectorをスカラーにします。例えば、
$$a=\left[
\begin{matrix}
1 \\
2 \\
3 \\
\end{matrix}\right] \qquad b=\left[
\begin{matrix}
4 \\
5 \\
6 \\
\end{matrix}\right]
$$
とすると、\(a\)と\(b\)の内積は
$$\begin{aligned}
a^T b &= \left[
\begin{matrix}
1 \quad 2 \quad 3 \\
\end{matrix}\right]
\left[
\begin{matrix}
4 \\
5 \\
6 \\
\end{matrix}\right] \\
&= (1)(4)+(2)(5)+(3)(6) \\
&= 32 \\
\end{aligned}$$
です。
また、\(a^T b = b^T a\)が成立します。

内積って角度に関連していたことしか覚えてないのですが、何かに使えるんですか?
内積を利用する例をいくつかあげると、
- 総和(sum): \(\mathbf{1}^T a = a_1 + …+a_n\)より、ベクトル\(a\)の総和を与えます。
- 平均(average): \((\mathbf{1}/n)^T a = (a_1 + …+a_n)/n\)より、\(a\)の平均を与えます。
- 平方和(sum of square): \(a^T a = a_1 ^2 +…+a_n ^2\)より、\(a\)の平方和を与えます。
- 共通部分(intersection): \(a = (1,0,0,1,1)\quad b = (0,0,1,1,1)\)の集合\(A, B\)において、\(a^T b =2\)より、\(A\cap B\)に含まれるオブジェクトが2つあることが分かります。
- 重み、特徴量、スコア(weights, features, score): \(f\)をオブジェクトの特徴量ベクトル、\(w\)を重みベクトルとすると、\(w^T f=s\)でスコアが計算できます。
- 多項式(polynomial evaluation): \(p(x)=c_1 + c_2 x + …+c_n x^{n-1}\)において、\( c = (c_1, c_2, …, c_n)、z=(1,t,t^2, …,t^{n-1})\)とすると、多項式は\(c^T z = p(t)\)とまとめられます。
などです。

機械学習を扱っていると、次第にベクトルの重要性に気づくと思います。
ノルム: Norm
ノルム(norm)は\(||x||\)と書き、ベクトルの長さ(大きさ)を表します。
ノルムはユークリッドノルム(\(L_2\)ノルム)を扱うことが多いです。
\(L_2\)ノルムの場合、$$\begin{aligned}||x||&=\sqrt{x_1^2 + x_2^2+…+x_n^2}\\
&=\sqrt{x^Tx}\end{aligned}$$
となります。
ノルムの性質として、以下4つが成立します。
- 非負均一性(Nonnegative homogeneity): \(||\beta x||=|\beta|||x||\)
- 三角不等式(Triangle inequality): \(||x+y|| \leq ||x||+||y||\)
- 非負(Nonnegavity): \(||x|| \geq 0\)
- 定値(Definiteness): \(||x|| = 0 \) if \(x = 0\)
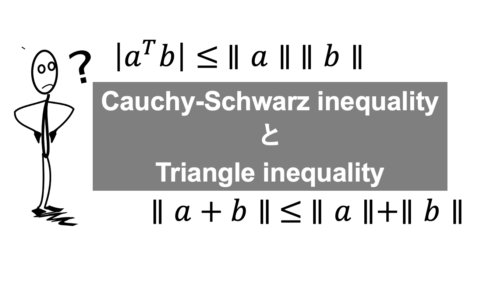
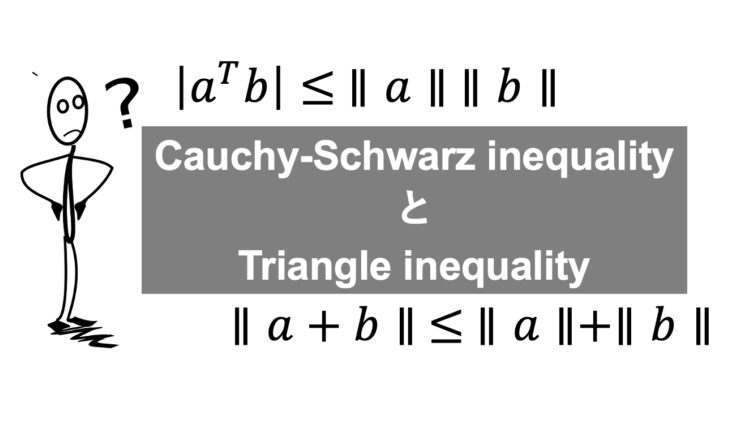
三角不等式の証明はこちら。

文字ばかりのベクトルの説明はここまで。「3Blue1Brown」からの動画を紹介します。視覚情報からベクトルを理解するのもいい方法だと思います。
Juliaでベクトルを扱う
最後にJuliaを使って「ベクトルの作成」「ベクトルの足し算・引き算・掛け算」「内積」「ノルム」を試します。
LinearAlgebraは線形代数に必要な操作を扱います。
このパッケージは以下のコードでインストールできます。
using Pkg
Pkg.add("Package Name")Juliaを使って少し感動したのは、Juliaが型を自動で予測する点です。v2_2にfloat型の要素がひとつ含まれているため、残りの2つの要素もfloat型になっています。
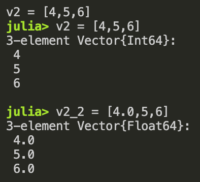
わざわざ型の指定をする必要がないのは楽チン!
ただ、時々この機能が本記事とは関係ないところで混乱を招くことも…。Juliaに慣れるのも時間がかかりそうです。
内積に関しては、上付きのカンマ'が付くとベクトルは\(v^T\)として転置されます。行列でも同じ扱いです。
norm()のデフォルトは、\(L_2\)ノルムを計算するよう設定されています。計算したいノルムの次元を変更することもできます。norm(v_1, 1)は\(L_1\)ノルムを返します。

今回はここまでです。pythonのnumpyも同様の操作ができますが、計算が目的なら、個人的にはJuliaの方がコードを短く書けるので好きです。
まとめ
今回はベクトルとJuliaの基本操作についてまとめました。
- ベクトルは1次元配列である
- 内積は、総和、平均、平方和などに利用される
- ノルムは、ベクトルの長さであり、ユークリッドノルムがよく利用される
- ノルムは非負、\(v=0\)のときだけノルムは0になる
- Juliaは型を指定しなくてもコードを書くことができる
- LinearAlgebraは線形代数に必要な機能を備えている

ありがとうございました。ベクトルって実生活でそんなに利用されているなんて気づけませんでした。私はてっきり難しい物理の世界だけかと…

私も高校・大学の数学は、ベクトル・行列といえば、正確に計算するところに意識がいっていました。多くの方にとって、まず、ベクトル・行列が現実の世界でどのように利用されているかを知ることが大事かもしれないですね。
参考文献
(2) Julia公式, “型” (6/15/2021アクセス)













この記事は、基本の復習のために「ベクトルの基本」と「ベクトルに関するJuliaの操作」をまとめます。(この章の内容は高校数学レベルなので、分かってる方は読み流してください)